
题目列表(包括答案和解析)
电焊工想利用一块边长为![]() 的正方形钢板
的正方形钢板![]() 做成一个扇形,于是设计了以下三种方案:
做成一个扇形,于是设计了以下三种方案:
方案一:如图1,直接从钢板上割下扇形![]() .
.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图4,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.
图1 图2 图3
1.容易得出图1、图3中所得扇形的圆心角均为![]() ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为![]() 吗?为什么?
吗?为什么?
2.容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
3.若将正方形钢板按类似图4的方式割成![]() 个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这
个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这![]() 个小扇形按类似方案三的方式焊接成一个大扇形,则当
个小扇形按类似方案三的方式焊接成一个大扇形,则当![]() 逐渐增大时,所焊接成的大扇形的面积如何变化?
逐渐增大时,所焊接成的大扇形的面积如何变化?
电焊工想利用一块边长为 的正方形钢板
的正方形钢板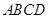 做成一个扇形,于是设计了以下三种方案:
做成一个扇形,于是设计了以下三种方案:
方案一:如图1,直接从钢板上割下扇形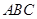 .
.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图4,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.
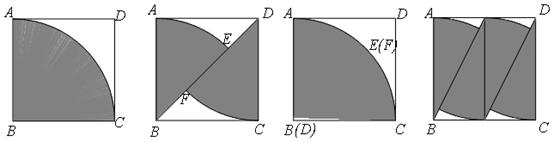
图1 图2 图3
1.容易得出图1、图3中所得扇形的圆心角均为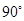 ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为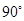 吗?为什么?
吗?为什么?
2.容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
3.若将正方形钢板按类似图4的方式割成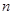 个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这
个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这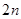 个小扇形按类似方案三的方式焊接成一个大扇形,则当
个小扇形按类似方案三的方式焊接成一个大扇形,则当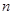 逐渐增大时,所焊接成的大扇形的面积如何变化?
逐渐增大时,所焊接成的大扇形的面积如何变化?
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a |
| b |
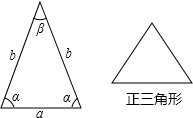 (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么? 电焊工想利用一块边长为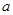 的正方形钢板
的正方形钢板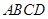 做成一个扇形,于是设计了以下三种方案:
做成一个扇形,于是设计了以下三种方案:
方案一:如图1,直接从钢板上割下扇形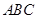 .
.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图4,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.
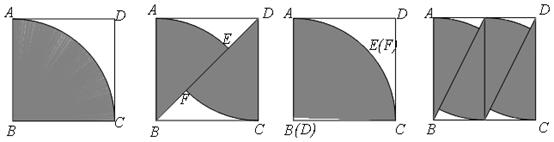
图1 图2 图3 图4
1.(1)容易得出图1、图3中所得扇形的圆心角均为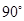 ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为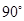 吗?为什么?
吗?为什么?
2.(2)容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
3.(3)若将正方形钢板按类似图4的方式割成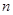 个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这
个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这 个小扇形按类似方案三的方式焊接成一个大扇形,则当
个小扇形按类似方案三的方式焊接成一个大扇形,则当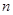 逐渐增大时,所焊接成的大扇形的面积如何变化?
逐渐增大时,所焊接成的大扇形的面积如何变化?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com