练习册

  • 练习册
  • 试题
    8．△ABC的三边长分别为5.12.13.与△ABC相似的△A′B′C′的最大边长为26.则△A′B′C′的周长为 ． 【查看更多】

     

    题目列表(包括答案和解析)

    △ABC的三边长分别为5、12、13，与它相似的△DEF的最小边长为15，求△DEF的其他两条边长和周长．

    查看答案和解析>>

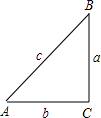    精英家教网如图，在△ABC中，∠C=90°，角A、B、C的对边分别为a、b、c，设△ABC的面积为s，周长的一半为l．
    （1）填写表：
    三边a、b、c l-a l-b s
    3、4、5 3 2 6
    5、12、13
    8、15、17
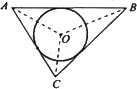
    （2）观察表，令m=l-a，n=l-b，探究m、n与s之间的关系，并对你的结论给予证明．

    查看答案和解析>>

    阅读材料：如图，△ABC的周长为l，内切圆O的半径为r，连结OA、OB、OC，△ABC被划分为三个小三角形，用S△ABC表示△ABC的面积

    ∵S△ABC＝S△OAB＋S△OBC＋S△OCA

    又∵S△OAB＝AB·r，S△OBC＝BC·r，S△OCA＝CA·r

    ∴S△ABC＝AB·r＋BC·r＋CA·r＝l·r(可作为三角形内切圆半径公式)

    (1)理解与应用：利用公式计算边长分为5、12、13的三角形内切圆半径；

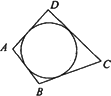
    (2)类比与推理：若四边形ABCD存在内切圆(与各边都相切的圆，如图)且面积为S，各边长分别为a、b、c、d，试推导四边形的内切圆半径公式；

    (3)拓展与延伸：若一个n边形(n为不小于3的整数)存在内切圆，且面积为S，各边长分别为a1、a2、a3、…an，合理猜想其内切圆半径公式(不需说明理由)．

    查看答案和解析>>

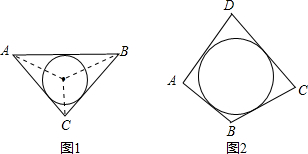    精英家教网阅读材料：如图1，△ABC的周长为l，面积为S，内切圆O的半径为r，探究r与S、l之间的关系．连接OA，OB，OC∵S=S△OAB+S△OBC+S△OCA
    又∵S△OAB=
    1
    2
    AB•r    ，S△OBC=
    1
    2
    BC•r    ，S△OCA=
    1
    2
    CA•r
    ∴S=
    1
    2
    AB•r+
    1
    2
    BC•r+
    1
    2
    CA•r=
    1
    2
    l•r
    ∴r=
    2S
    l

    解决问题：
    （1）利用探究的结论，计算边长分别为5，12，13的三角形内切圆半径；
    （2）若四边形ABCD存在内切圆（与各边都相切的圆），如图2且面积为S，各边长分别为a，b，c，d，试推导四边形的内切圆半径公式；
    （3）若一个n边形（n为不小于3的整数）存在内切圆，且面积为S，各边长分别为a1，a2，a3，…，an，合理猜想其内切圆半径公式（不需说明理由）．

    查看答案和解析>>

    在△ABC中，∠C=90°，周长为60，斜边与一条直角边的比为13:5，则这个三角形的三边长分别为(  　)

    A．5、4、3               B．13、12、5           C．10、8、6            D．26、24、10

    查看答案和解析>>


    同步练习册答案