练习册

  • 练习册
  • 试题
    16．对于正方体ABCD-A1B1C1D1.则下面命题:①P在直线BC1上运动时.三棱锥A-D1PC的体积不变,②P在直线BC1上运动时.二面角P-AD1-C的大小不变,③P在直线BC1上运动时.直线AP与平面ACD1所成角的大小不变,④M是平面A1B1C1D1上到点D和点C1距离相等的点.则M点的轨迹是过点D1的抛物线.其中真命题的编号是 . 【查看更多】

     

    题目列表(包括答案和解析)

    正方体ABCD，A1B1C1D1中，E、F分别是BB1、CC1的中点，则AE、BF所成的角的余弦值是（　　）
    A、-
    1
    5
    B、
    2
    		6
    5
    C、
    1
    5
    D、
    2
    5

    查看答案和解析>>

    （理）已知正方体ABCD一A1B1C1D1的棱长为1，则BC1与DB1的距离为（　　）

    查看答案和解析>>

    5.在棱长为1的正方体ABCD－A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G=(0≤≤1)，则点G到平面D1EF的距离为

    A.                                                                    B.

    C.                                                                  D.

    查看答案和解析>>

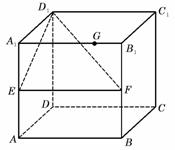
    正方体ABCD－A1B1C1D1中，E为BC1的中点，则异面直线A1E与CD1所成角等于

    A．90°     B．60°     C．45°     D．30°

     

    查看答案和解析>>

    在正方体ABCD－A1B1C1D1中，E、F是分别是棱A1B1、A1D1的中点，则A1B与EF所成角的大小为__________

     

    查看答案和解析>>

     

    一、选择题

    1、C       2、C        3、D       4、B       5、D       6、A  

    7、D       8、B        9、C      10、A      11、B      12、B

    二、填空题

    13、±4         14、0.18       15、251，4      16、①②

    三、解答题

    17、解：（Ⅰ）由，得

    即

    也即

    ∴

    ∴   ∴

    （Ⅱ）∵  

    ∴的最大值为

    18、解：（Ⅰ）∵击中目标次的概率为

    ∴他至少击中两次的概率

    （Ⅱ）设转移前射击次数为，的可能取值为1，2，3，4，5

    则，1，2，3，4   

    ∴的分布列为

    1

    2

    3

    4

    5

    ∴

    19、解：（Ⅰ）∵面，∴面

    作于M，连OM

    ∴是二面角B－DE－A的平面角，

    在中，，，由等面积法得

    又   ∴

    ∴

    （Ⅱ）     ∴

    设为直线BC与平面EDB所成的角，则

    20．解：（Ⅰ）由已知得

    依题意：对恒成立

    即：对恒成立

    也即：对恒成立

    ∴    即

    （Ⅱ）∵

    ∴在定义域上

    满足在上是减函数，在是增函数

      当时，，∴在上是增函数

      当时，，∴在上是减函数

      当时，，∴在上是减函数

    在上是增函数

    21、解：（Ⅰ）设切点A、B的坐标为、

    则过A、B的圆的切线方程分别为：

       

    ∴两切线均过点，且

    ∴，由此可知点A、B都在直线上

    ∴直线的方程为

    （Ⅱ）设，由（Ⅰ）可知直线AB的方程为

    令得，即，同理可得

    ∴，即为……①

    ∵P在椭圆上，∴

    又，代入①式，得

    故椭圆C的方程为：

    22、解：（Ⅰ）∵，∴

    两式相减得：

    即    ∴

    ∴时，

    又，∴

    （Ⅱ）证明：

    又

    ∴

    而

    ∴

    （Ⅲ）

    ∴


    同步练习册答案