练习册

  • 练习册
  • 试题
    (Ⅱ)求证:, 【查看更多】

     

    题目列表(包括答案和解析)

    （Ⅰ）求证：；
    （Ⅱ）化简：．

    查看答案和解析>>

    （Ⅰ）求证：；
    （Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；  
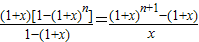    （Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．

    查看答案和解析>>

    （Ⅰ）求证：
    sinx
    1-cosx
    =
    1+cosx
    sinx
    ；
    （Ⅱ）化简：
    tan(3π-α)
    sin(π-α)sin(
    3
    2
    π-α)
    +
    sin(2π-α)cos(α-
    7π
    2
    )
    sin(
    3π
    2
    +α)cos(2π+α)
    ．

    查看答案和解析>>

    （Ⅰ）求证：
    C
    m
    n
    =
    n
    m
    C
    m-1
    n-1
    ；
    （Ⅱ）利用第（Ⅰ）问的结果证明Cn1+2Cn2+3Cn3+…+nCnn=n•2n-1；  
    （Ⅲ）其实我们常借用构造等式，对同一个量算两次的方法来证明组合等式，譬如：（1+x）1+（1+x）2+（1+x）3+…+（1+x）n=
    (1+x)[1-(1+x)n]
    1-(1+x)
    =
    (1+x)n+1-(1+x)
    x
    ；，由左边可求得x2的系数为C22+C32+C42+…+Cn2，利用右式可得x2的系数为Cn+13，所以C22+C32+C42+…+Cn2=Cn+13．请利用此方法证明：（C2n0）2-（C2n1）2+（C2n2）2-（C2n3）2+…+（C2n2n）2=（-1）nC2nn．

    查看答案和解析>>

    （Ⅰ）求证：
    sinx
    1-cosx
    =
    1+cosx
    sinx
    ；
    （Ⅱ）化简：
    tan(3π-α)
    sin(π-α)sin(
    3
    2
    π-α)
    +
    sin(2π-α)cos(α-
    7π
    2
    )
    sin(
    3π
    2
    +α)cos(2π+α)
    ．

    查看答案和解析>>

     

    一、选择题

    1、C       2、C        3、D       4、B       5、D       6、A  

    7、D       8、B        9、C      10、A      11、B      12、B

    二、填空题

    13、±4         14、0.18       15、251，4      16、①②

    三、解答题

    17、解：（Ⅰ）由，得

    即

    也即

    ∴

    ∴   ∴

    （Ⅱ）∵  

    ∴的最大值为

    18、解：（Ⅰ）∵击中目标次的概率为

    ∴他至少击中两次的概率

    （Ⅱ）设转移前射击次数为，的可能取值为1，2，3，4，5

    则，1，2，3，4   

    ∴的分布列为

    1

    2

    3

    4

    5

    ∴

    19、解：（Ⅰ）∵面，∴面

    作于M，连OM

    ∴是二面角B－DE－A的平面角，

    在中，，，由等面积法得

    又   ∴

    ∴

    （Ⅱ）     ∴

    设为直线BC与平面EDB所成的角，则

    20．解：（Ⅰ）由已知得

    依题意：对恒成立

    即：对恒成立

    也即：对恒成立

    ∴    即

    （Ⅱ）∵

    ∴在定义域上

    满足在上是减函数，在是增函数

      当时，，∴在上是增函数

      当时，，∴在上是减函数

      当时，，∴在上是减函数

    在上是增函数

    21、解：（Ⅰ）设切点A、B的坐标为、

    则过A、B的圆的切线方程分别为：

       

    ∴两切线均过点，且

    ∴，由此可知点A、B都在直线上

    ∴直线的方程为

    （Ⅱ）设，由（Ⅰ）可知直线AB的方程为

    令得，即，同理可得

    ∴，即为……①

    ∵P在椭圆上，∴

    又，代入①式，得

    故椭圆C的方程为：

    22、解：（Ⅰ）∵，∴

    两式相减得：

    即    ∴

    ∴时，

    又，∴

    （Ⅱ）证明：

    又

    ∴

    而

    ∴

    （Ⅲ）

    ∴


    同步练习册答案