
题目列表(包括答案和解析)
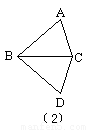
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.



政府根据社会需要,对自来水价格举行了听证会,决定从今年4月份起对自来水价格进行调整,调整后生活用水价格的部分信息如下表:
|
用水量(m3) |
单价(元∕m3) |
|
5m3以内(包括5m3)的部分 |
2 |
|
5m3以上的部分 |
|
已知5月份小晶家和小磊家分别交水费19元、31元,且小磊家的用水量是小晶家的用水量的1.5倍,请你通过上述信息,求出表中的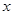 。
。
| 班级 | 一班 | 二班 | 三班 |
| 金额(元) | 2000 |  | |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com