
题目列表(包括答案和解析)

 (2012•深圳模拟)如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度
(2012•深圳模拟)如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度 你会数线段吗?
你会数线段吗?| 1×2 |
| 2 |
| 2×3 |
| 2 |
| 3×4 |
| 2 |
| (n+1)(n+2) |
| 2 |
| (n+1)(n+2) |
| 2 |
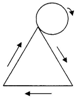 (2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
(2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了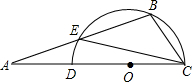 (2006•河北区一模)如图,DC是半圆O的直径,若∠A=20°,∠BCE=40°,则∠BEC等于( )
(2006•河北区一模)如图,DC是半圆O的直径,若∠A=20°,∠BCE=40°,则∠BEC等于( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com