
题目列表(包括答案和解析)
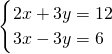 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组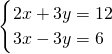 有唯一解.
有唯一解. =4-
=4- x
x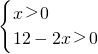 则有0<x<6
则有0<x<6 x为正整数,则
x为正整数,则 x为正整数,所以x为3的倍数.
x为正整数,所以x为3的倍数. ×3=2
×3=2
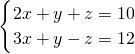 的正整数解.
的正整数解.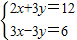 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组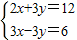 有唯一解.
有唯一解.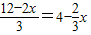
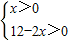 则有0<x<6
则有0<x<6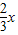 为正整数,则
为正整数,则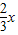 为正整数,所以x为3的倍数
为正整数,所以x为3的倍数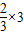 =2
=2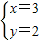
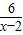 为正整数,则满足条件的x的值有几个.( )
为正整数,则满足条件的x的值有几个.( )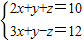 的正整数解.
的正整数解.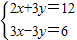 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组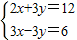 有唯一解.
有唯一解.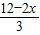 =4-
=4- x
x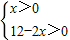 则有0<x<6
则有0<x<6 x为正整数,则
x为正整数,则 x为正整数,所以x为3的倍数.
x为正整数,所以x为3的倍数. ×3=2
×3=2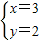
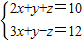 的正整数解.
的正整数解.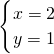 ,所以在平面直角坐标系中就可以用点(2,1)表示它的一个解,
,所以在平面直角坐标系中就可以用点(2,1)表示它的一个解, 的图象(画在图中)、由这两个二元一次方程的图象,能得出这个二元一次方程组的解吗?请将表示其解的点P标在平面直角坐标系中,并写出它的坐标.
的图象(画在图中)、由这两个二元一次方程的图象,能得出这个二元一次方程组的解吗?请将表示其解的点P标在平面直角坐标系中,并写出它的坐标.
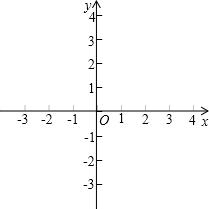 在同一坐标系中画出函数y=2x+1和y=-2x+1的图象,并利用图象写出二元一次方程组
在同一坐标系中画出函数y=2x+1和y=-2x+1的图象,并利用图象写出二元一次方程组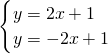 的解.
的解.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com