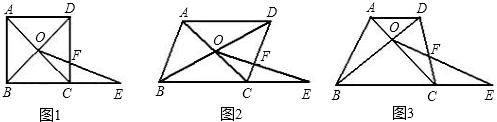
(2010•卢湾区二模)数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线--过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
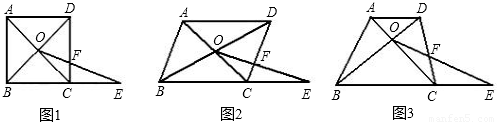
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
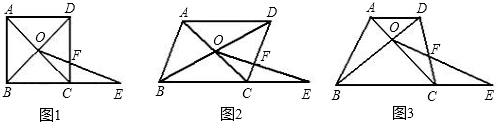
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.


 AC,试说明△ABC是直角三角形.
AC,试说明△ABC是直角三角形.