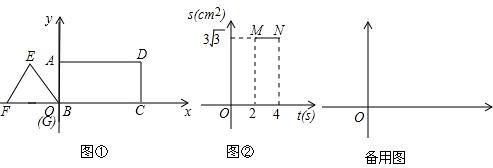
在平面直角坐标系中,矩形ABCD与等边△EFG按如图①所示放置:点B、G与坐标原点O重合,F、B、G、C在x轴上,E、A、D三点同在平行于x轴的直线上.△EFG沿x轴向右匀速移动,当点G移至与点C重合时,△EFG即停止移动.在△EFG移动过程中,与矩形ABCD的重合部分的面积S(cm
2)与移动时间t(s)的一部分函数图象是线段MN如图②所示(即△EFG完全进入矩形ABCD内部时的一段函数图象)
(1)结合图②,求等边△EFG的边长和它移动的速度;
(2)求S与t的函数关系式,并在图②中补全△EFG在整个移动过程中,S与t的函数关系式的大致图象;
(3)当△EFG移动(
+1)s时,E点到达P点的位置,一开口向下的抛物线y=
x2+bx,过P、O两点且与射线AD相交于点H,与x轴相交于点Q(异于原点).请问a是否存在取某一值或某一范围,使OQ+PH的值为定值?如果存在,求出a值或a的取值范围;如果不存在,请说明理由.

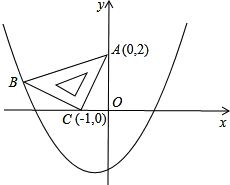 两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.
两坐标轴上,且点A(0,2),点C(-1,0),如图所示;抛物线y=ax2+ax-2经过点B.