
题目列表(包括答案和解析)
在直角三角形中,若一个锐角为300,斜边与较小直角边的和为18cm,则较大直角边为 cm.
在直角三角形中,若一个锐角为300,斜边与较小直角边的和为18cm,则较大直角边为 cm.
(本小题满分7分)
(1)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=300,求BC的长。(结果保留根号)

(2)如图,已知平行四边形ABCD中,点![]() 为
为![]() 边的中点, 延长
边的中点, 延长![]() 相交于点
相交于点![]() .
.
求证: .
.

【解析】(1)直角三角形中是已知一个锐角和一条边,根据三角函数就可以求出(2)欲证CD=BF,需证△CDE≌△BFE.由于四边形ABCD是平行四边形,所以DC∥BF,∠1=∠3,∠C=∠2.又点E为BC边的中点,根据AAS,所以△CDE≌△BFE
(本小题满分7分)
(1)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=300,求BC的长。(结果保留根号)

(2)如图,已知平行四边形ABCD中,点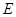 为
为 边的中点, 延长
边的中点, 延长 相交于点
相交于点 .
.
求证: .
.

【解析】(1)直角三角形中是已知一个锐角和一条边,根据三角函数就可以求出(2)欲证CD=BF,需证△CDE≌△BFE.由于四边形ABCD是平行四边形,所以DC∥BF,∠1=∠3,∠C=∠2.又点E为BC边的中点,根据AAS,所以△CDE≌△BFE
 现在初中课本里所学习的概率计算问题只有以下类型:
现在初中课本里所学习的概率计算问题只有以下类型:| 第1组 试验 |
第2组 试验 |
第3组 试验 |
第4组 试验 |
第5组 试验 | |
| 构成锐角三角形次数 | 86 | 158 | 250 | 337 | 420 |
| 构成直角三角形次数 | 2 | 5 | 8 | 10 | 12 |
| 构成钝角三角形次数 | 73 | 155 | 191 | 258 | 331 |
| 不能构成三角形次数 | 139 | 282 | 451 | 595 | 737 |
| 小计 | 300 | 600 | 900 | 1200 | 1500 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com