一个两位数的数字之和为11，十位数字与个位数字互换后，所得新数比原数小45，则原两位数是多少？

（2013•南京二模）阅读材料，回答问题：
如果二次函数y₁的图象的顶点在二次函数y₂的图象上，同时二次函数y₂的图象的顶点在二次函数y₁的图象上，那么我们称y₁的图象与y₂的图象相伴随．
例如：y=（x+1）²+2图象的顶点（-1，2）在y=-（x+3）²+6的图象上，同时y=-（x+3）²+6图象的顶点
（-3，6）也在y=（x+1）²+2的图象上，这时我们称这两个二次函数的图象相伴随．

（1）说明二次函数y=x²-2x-3的图象与二次函数y=-x²+4x-7的图象相伴随；
（2）如图，已知二次函数y₁=

1

4

（x+1）²-2图象的顶点为M，点P是x轴上一个动点，将二次函数y₁的图象绕点P旋转180°得到一个新的二次函数y₂的图象，且旋转前后的两个函数图象相伴随，y₂的图象的顶点为N．
①求二次函数y₂的关系式；
②以MN为斜边作等腰直角△MNQ，问y轴上是否存在满足要求的点Q？若存在，求出Q点的坐标；若不存在，请说明理由．

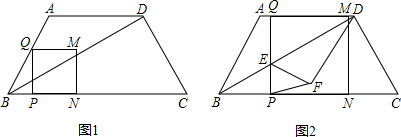
如图1，梯形ABCD中，AD∥BC，AB=AD=DC=5，BC=11．一个动点P从点B出发，以每秒1个单位长度的速度沿线段BC方向运动，过点P作PQ⊥BC，交折线段BA-AD于点Q，以PQ为边向右作正方形PQMN，点N在射线BC上，当Q点到达D点时，运动结束．设点P的运动时间为t秒（t＞0）．
（1）当正方形PQMN的边MN恰好经过点D时，求运动时间t的值；
（2）在整个运动过程中，设正方形PQMN与△BCD的重合部分面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；
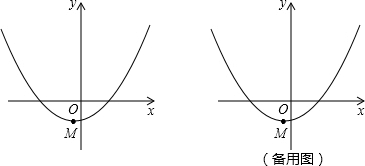
（3）如图2，当点Q在线段AD上运动时，线段PQ与对角线BD交于点E，将△DEQ沿BD翻折，得到△DEF，连接PF．是否存在这样的t，使△PEF是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．