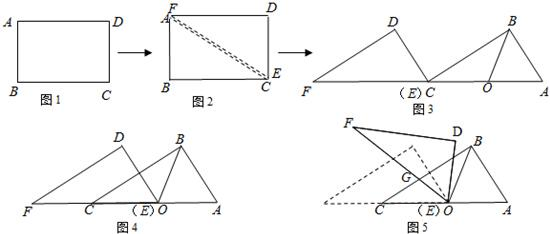
将一张矩形纸片沿对角线剪开(如图1),得到两张三角形纸片△ABC、△DEF(如图2),量得他们的斜边长为6cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,且点A、C、E、F在同一条直线上,点C与点E重合.△ABC保持不动,OB为△ABC的中线.现对△DEF纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△DEF沿CA向右平移,直到两个三角形完全重合为止.设平移距离CE为x(即CE的长),求平移过程中,△DEF与△BOC重叠部分的面积S与x的函数关系式,以及自变量的取值范围;
(2)△DEF平移到E与O重合时(如图4),将△DEF绕点O顺时针旋转,旋转过程中△DEF的斜边EF交△ABC的BC边于G,求点C、O、G构成等腰三角形时,△OCG的面积;
(3)在(2)的旋转过程中,△DEF的边EF、DE分别交线段BC于点G、H(不与端点重合).求旋转角∠COG为多少度时,线段BH、GH、CG之间满足GH
2+BH
2=CG
2,请说明理由.
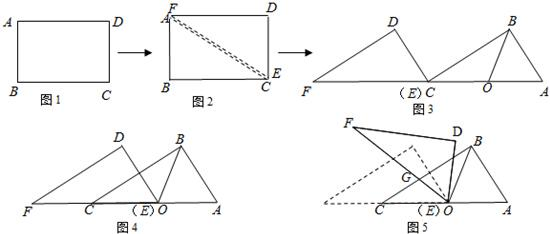

 13、如图三角形ABC全等于三角形DEF,CE=3,则AF=
13、如图三角形ABC全等于三角形DEF,CE=3,则AF=
 22、填空,完成下列证明过程.
22、填空,完成下列证明过程.