在△ABC中，若∠A=30°，∠B=60°，则这个三角形为三角形；若∠A：∠B：∠C=1：3：5，这个三角形为三角形．（按角的分类填写）

直角三角形是一个奇妙的三角形，除了有勾股定理这样著名的定理外，它还有许多奇妙的特性值得我们去探索，例如，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c．设S_△ABC=S，a+b+c=l，则S与l的比

蕴含着一个奇妙的规律，这个规律与a+b-c的值有关，观察下面a、b、c取具体勾股数的表：

若a+b-c=m，则观察上表我们可以猜想出

（用含m的代数式表示）

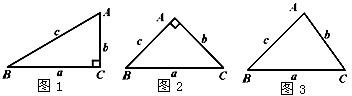
如图1，在ΔABC中，∠A＝2∠B，且∠A＝60°．小明通过以下计算：由题意，∠B＝30°，∠C＝90°，c＝2b，a＝b，得a²－b²＝(b)²－b²＝2b²＝b?c．即a²－b²＝ bc．

于是，小明猜测：对于任意的ΔABC，当∠A＝2∠B时，关系式a²－b²＝bc都成立．

（1）如图2，请你用以上小明的方法，对等腰直角三角形进行验证，判断小明的猜测是否正确，并写出验证过程；

（2）如图3，你认为小明的猜想是否正确，若认为正确，请你证明；否则，请说明理由；

（3）若一个三角形的三边长恰为三个连续偶数，且∠A＝2∠B，请直接写出这个三角形三边的长，不必说明理由．

27、我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．
（1）写出你所知道的特殊四边形中是勾股四边形的两种图形的名称

正方形

，

长方形

．
（2）如下图（1），请你在图中画出以格点为顶点，OA、OB为勾股边，且对角线相同的所有勾股四边形OAMB．
（3）如图（2），以△ABC边AB作如图正三角形ABD，∠CBE=60°，且BE=BC，连接DE、DC，∠DCB=30°．求证：DC²+BC²=AC²，即四边形ABCD是勾股四边形．

同步练习册答案

在△ABC中，若∠A=30°，∠B=60°，则这个三角形为________三角形；若∠A：∠B：∠C=1：3：5，这个三角形为________三角形．（按角的分类填写）