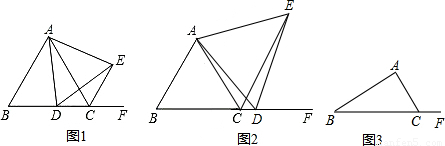
已知:在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的左侧作等腰直角△ADE,解答下列各题:
(1)如果AB=AC,∠BAC=90°.
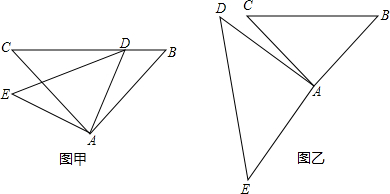
(i)当点D在线段BC上时(与点B不重合),如图甲,线段BD,CE之间的位置关系为
BD⊥CE,且BD=CE.
BD⊥CE,且BD=CE.
(ii)当点D在线段BC的延长线上时,如图乙,i)中的结论是否还成立?为什么?
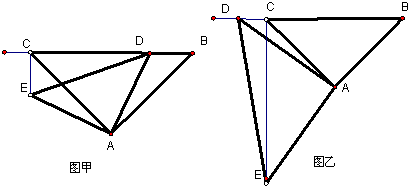
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,BC⊥CE(点D不与点C,B重合)?试画出相应图形,写出你的探究结果(不用证明).