练习册

  • 练习册
  • 试题
    (1)∵OA＝OB＝OC.∠AOC＝∠BOC＝90° ∴∠OAC＝∠OCA＝∠OBC＝∠OCB＝45° ∴∠ACB＝90° --1分 又△ABC的面积为9. ∴OA＝OC＝OB＝3 --2分 ∴A --4分 (2)当t＝3秒时.即CP＝OC时.DP与DB垂直且相等. --5分 理由如下: 连结OD.作DM⊥x轴于点M.作DN⊥y轴于点N ∵D ∴DM＝DN＝OM＝ON＝m ∴∠DOM＝∠DON＝45° 而∠ACO＝45° ∴DC＝DO ∴∠PCD＝∠BOD＝135° 又CP＝OC＝OB ∴△PCD≌△BOD (SAS) --7分 ∴DP＝DB.∠PDC＝∠BDO ∴∠BDP＝∠ODC＝90° 即DP⊥DB. --8分 (3)解:①正确. 在QA上截取QS＝QP.连结PS. --9分 ∵∠PQA＝60° ∴△QSP是等边三角形 ∴PS＝PQ.∠SPQ＝60° ∵PO是AB的垂直平分线 ∴PA＝PB 而PA＝AB ∴PA＝PB＝AB ∴∠APB＝60° ∴∠APS＝∠BPQ ∴△APS≌△BPQ --11分 ∴∠PAS＝∠PBQ ∴∠APQ+∠PBQ＝∠APQ+∠PAS＝180° --12分 注:不同于此标答的解法请参照此标答给分. 【查看更多】

     

    题目列表(包括答案和解析)

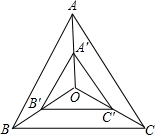    精英家教网如图：点O是等边△ABC的中心，A′、B′、C′分别是OA，OB，OC的中点，则△ABC与△A′B′C′是位似三角形，此时，△A′B′C′与△ABC的位似比、位似中心分别为（　　）
    A、
    1
    2
    ，点A′
    B、2，点A
    C、
    1
    2
    ，点O
    D、2，点O

    查看答案和解析>>

    如图：点O是等边△ABC的中心，A′、B′、C′分别是OA，OB，OC的中点，则△ABC与△A′B′C′是位似三角形，此时，△A′B′C′与△ABC的位似比、位似中心分别为（　　）
    A．
    1
    2
    ，点A′    		B．2，点AC．
    1
    2
    ，点O    		D．2，点O
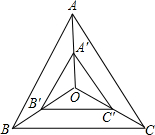
    精英家教网

    查看答案和解析>>

    如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D，E，F分别是OA，OB，OC的四等分点，则△DEF与△ABC的面积比是（    ）

    A．1：4  B．1：8  C．1：16   D．1：12

     


    查看答案和解析>>

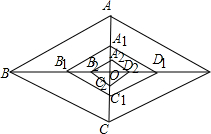    精英家教网如图，菱形ABCD的面积为l，对角线AC，BD交于点O，点Al，Bl，Cl，Dl分别是OA，OB，OC，OD的中点，连接AlBl，BlCl，ClDl，DlAl得到菱形AlBlClDl；点A2，B2，C2，D2分别是OAl，OBl，OCl，ODl的中点，连接A2B2，B2C2，C2D2，D2A2，得到菱形A2B2C2D2；…，依此类推，则菱形A2009B2009C2009D2009的面积为
     
    ．

    查看答案和解析>>

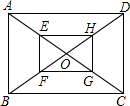    精英家教网如图所示，矩形ABCD的对角线AC，BD相交于点O，E，F，G，H分别是OA，OB，OC，OD的中点，求证：四边形EFGH是矩形．

    查看答案和解析>>


    同步练习册答案