（本小题6分）如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形。

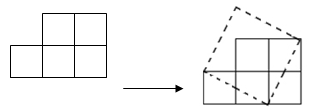
1.拼成的正方形的面积与边长分别是多少？

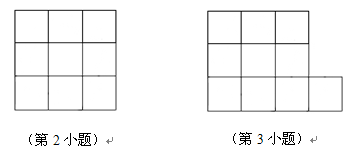
2.你能在3×3方格图中，连接四个格点组成面积为5的正方形吗？

3.你能把十个小正方形组成的图形纸，剪开并拼成正方形吗?若能，则它的边长是多少？

（本小题6分）如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形。

1.拼成的正方形的面积与边长分别是多少？

2.你能在3×3方格图中，连接四个格点组成面积为5的正方形吗？

3.你能把十个小正方形组成的图形纸，剪开并拼成正方形吗?若能，则它的边长是多少？

（本题满分9分）如图①，小慧同学把一个正三角形纸片（即△OAB）放在直线l₁上，OA边与直线l₁重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O₁处，点B运动到了点B₁处；小慧又将三角形纸片AO₁B₁绕点B₁按顺时针方向旋转120°，此时点A运动到了点A₁处，点O₁运动到了点O₂处（即顶点O经过上述两次旋转到达O₂处）．

    小慧还发现：三角形纸片在上述两次旋转的过程中，顶点O运动所形成的图形是两段

圆弧，即和，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧

与直线l₁围成的图形面积等于扇形AOO₁的面积、△AO₁B₁的面积和扇形B₁O₁O₂的面积之

和．

    小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l₂上，OA

边与直线l₂重合，然后将正方形纸片绕着顶点^按顺时针方向旋转90°，此时点O运动到

了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处；小慧又将正方形

纸片AO₁C₁B₁绕顶点B₁按顺时针方向旋转90°，……，按上述方法经过若干次旋转后．她

提出了如下问题：

     问题①：若正方形纸片OABC接上述方法经过3次旋转，求顶点O经过的路程，并

求顶点O在此运动过程中所形成的图形与直线l₂围成图形的面积；若正方形纸片OA BC

按上述方法经过5次旋转，求顶点O经过的路程；

     问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是

?

       请你解答上述两个问题．

（本题满分9分）如图①，小慧同学把一个正三角形纸片（即△OAB）放在直线l₁上，OA边与直线l₁重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O₁处，点B运动到了点B₁处；小慧又将三角形纸片AO₁B₁绕点B₁按顺时针方向旋转120°，此时点A运动到了点A₁处，点O₁运动到了点O₂处（即顶点O经过上述两次旋转到达O₂处）．
小慧还发现：三角形纸片在上述两次旋转的过程中，顶点O运动所形成的图形是两段
圆弧，即和，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧
与直线l₁围成的图形面积等于扇形AOO₁的面积、△AO₁B₁的面积和扇形B₁O₁O₂的面积之
和．
小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l₂上，OA
边与直线l₂重合，然后将正方形纸片绕着顶点^按顺时针方向旋转90°，此时点O运动到
了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处；小慧又将正方形
纸片AO₁C₁B₁绕顶点B₁按顺时针方向旋转90°，……，按上述方法经过若干次旋转后．她
提出了如下问题：
问题①：若正方形纸片OABC接上述方法经过3次旋转，求顶点O经过的路程，并
求顶点O在此运动过程中所形成的图形与直线l₂围成图形的面积；若正方形纸片OA BC
按上述方法经过5次旋转，求顶点O经过的路程；
问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是
?
请你解答上述两个问题．