
题目列表(包括答案和解析)
| 由多项式的乘法法则知:若(x+a)(x+b)=x2+x+q,则p=a+b,q=a·b;反过来x2+x+q=(x+a)(x+b)要将多项式x2+x+q进行分解,关键是找到两个数a、b,使a+b=p,a·b=q,如对多项式x2-3x+2,有p=-3,q=2,a=-1,b=-2。此时(-1)+(-2)=-3,(-1)(-2)=2,所以x2-3x+2可分解为(x-1)(x-2)即x2-3x-2=(x-1)(x-2)。 (1)根据以上填写下表: | ||||||||||||||||||||||||||||||
当q是正数时,应分解成两个因数a、b_______________号,a、b的符号与__________相同; 当q是负数时,应分解成的两个因数a、b______________号,a、b中绝对值较大的因数的符号与_______相同。 (3)分解因式: x2-x-12=_____________;x2-7x+6=________________。 |
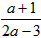 有意义,则a的值应是( );要使分式
有意义,则a的值应是( );要使分式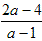 的值为零,则a的值应为( )。
的值为零,则a的值应为( )。| 某精品水果超市销售一种进口水果A,从去年1至7月,这种水果的进价一路攀升,每千克A的进价y1与月份x(1≤x≤7,且x为整数),之间的函数关系式如下表: | ||||||||||||||||
(1)请观察表格和图像,用所学过的一次函数、反比例函数、二次函数的有关知识分别写出y1与x和y2与x的函数关系式。 | ||||||||||||||||
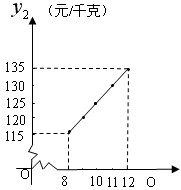 | ||||||||||||||||
| (2)若去年该水果的售价为每千克180元,且销售该水果每月必须支出(除进价外)的固定支出为300元,已知该水果在1月至7月的销量p1(千克)与月份x满足:p1=10x+80;8月至12月的销量p2(千克)与月份x满足:p2=-10x+250;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润。 (3)今年1月到6月,该进口水果的进价进行调整,每月进价均比去年12月的进价上涨15元,且每月的固定支出(除进价外)增加了15%,已知该进口水果的售价在去年的基础上提高了a%(a<100),与此同时每月的销量均在去年12月的基础上减少了0.2a%,这样销售下去要使今年1至6月的总利润为68130元,试求出a的值。(保留两个有效数字)(参考数据:232=529,242=576,252=625,262=676) |
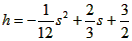 ,如图,已知球网AB距原点5m,乙扣球的最大高度(用线段CD表示)为
,如图,已知球网AB距原点5m,乙扣球的最大高度(用线段CD表示)为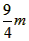 ,设乙的起跳点C的横坐标为m,乙原地起跳,因球的高度高于乙扣球的最大高度会导致接球失败,若甲要使乙接球失败,则m的取值范围是( )。
,设乙的起跳点C的横坐标为m,乙原地起跳,因球的高度高于乙扣球的最大高度会导致接球失败,若甲要使乙接球失败,则m的取值范围是( )。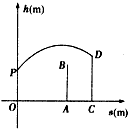
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com