21、我们在解决数学问题时，经常采用“转化”（或“化归”）的思想方法，把待解决的问题，通过某种转化过程，归结到一类已解决或比较容易解决的问题．
譬如，在学习了一元一次方程的解法以后，进一步研究二元一次方程组的解法时，我们通常采用“消元”的方法，把二元一次方程组转化为一元一次方程；再譬如，在学习了三角形内角和定理以后，进一步研究多边形的内角和问题时，我们通常借助添加辅助线，把多边形转化为三角形，从而解决问题．
问题提出：如何把一个正方形分割成n（n≥9）个小正方形？
为解决上面问题，我们先来研究两种简单的“基本分割法”．
基本分割法1：如图①，把一个正方形分割成4个小正方形，即在原来1个正方形的基础上增加了3个正方形．
基本分割法2：如图②，把一个正方形分割成6个小正方形，即在原来1个正方形的基础上增加了5个正方形．
问题解决：有了上述两种“基本分割法”后，我们就可以把一个正方形分割成n（n≥9）个小正方形．
（1）把一个正方形分割成9个小正方形．
一种方法：如图③，把图①中的任意1个小正方形按“基本分割法2”进行分割，就可增加5个小正方形，从而分割成4+5=9（个）小正方形．
另一种方法：如图④，把图②中的任意1个小正方形按“基本分割法1”进行分割，就可增加3个小正方形，从而分割成6+3=9（个）小正方形．
（2）把一个正方形分割成10个小正方形．
方法：如图⑤，把图①中的任意2个小正方形按“基本分割法1”进行分割，就可增加3×2个小正方形，从而分割成4+3×2=10（个）小正方形．
（3）请你参照上述分割方法，把图⑥给出的正方形分割成11个小正方形（用钢笔或圆珠笔画出草图即可，不用说明分割方法）
（4）把一个正方形分割成n（n≥9）个小正方形．
方法：通过“基本分割法1”、“基本分割法2”或其组合把一个正方形分割成9个、10个和11个小正方形，再在此基础上每使用1次“基本分割法1”，就可增加3个小正方形，从而把一个正方形分割成12个、13个、14个小正方形，依次类推，即可把一个正方形分割成n（n≥9）个小正方形．
从上面的分法可以看出，解决问题的关键就是找到两种基本分割法，然后通过这两种基本分割法或其组合把正方形分割成n（n≥9）个小正方形．
类比应用：仿照上面的方法，我们可以把一个正三角形分割成n（n≥9）个小正三角形．
（1）基本分割法1：把一个正三角形分割成4个小正三角形（请你在图a中画出草图）；
（2）基本分割法2：把一个正三角形分割成6个小正三角形（请你在图b中画出草图）；
（3）分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形（用钢笔或圆珠笔画出草图即可，不用说明分割方法）；
（4）请你写出把一个正三角形分割成n（n≥9）个小正三角形的分割方法（只写出分割方法，不用画图）．
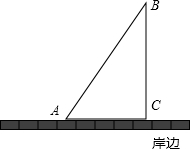一天，小明去某海滨浴场游泳，当他游到离岸边AC 300米的B处（即BC⊥AC于C，且BC=300米）时，发生了抽筋，岸上观察哨A处的一救生员接到求救信号，他有两种营救方式：
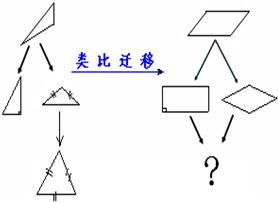13、从一般到特殊是一种重要的数学思想，右图通过类比的方法展现了认识三角形与平行四边形图形特征的过程，你认为“？”处的图形名称是
【老题重现】
