
题目列表(包括答案和解析)
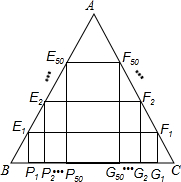 (2011•杭州一模)如图,在△ABC中,AB=AC=
(2011•杭州一模)如图,在△ABC中,AB=AC=| 5 |
如图,在直径为AB的圆内,划出一块三角形区域使三角形的一边为AB,顶点C在半圆上,其他两边分别为6和8,现在建造一个内接内△ABC的矩形水池DEFN,其中DE在AB上,如图的设计方案是AC=8,BC=6.
?
(1)求△ABC中AB边上的高h;
(2)设DN=x,当x为何值时,水池DEFN的面积最大?
(3)实施施工时,发现在AB边上距B点1.85m处的M处有一棵大树,这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开这棵大树.
 已知:如图所示,在△ABC中,BC=100,边BC上的高为50.在这个三角形内有一个内接矩形PQRS.
已知:如图所示,在△ABC中,BC=100,边BC上的高为50.在这个三角形内有一个内接矩形PQRS.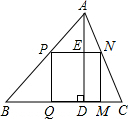 其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少mm?”
其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少mm?”九年级上册的教材第118页有这样一道习题:
“在一块三角形余料ABC中,它的边BC=120mm,高线AD=80mm.要把它加工成正方形零件(如图),使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少mm?”
(1)请你解答上题;
(2)若将上题图中的正方形PQMN改为矩形,其余条件不变,求矩形PQMN的面积S的最大值;
(3)我们把上面习题中的正方形PQMN叫做“BC边上的△ABC的内接正方形”,若在习题的条件下,又知AB=150mm,AC=100mm,请分别写出AB边上的△ABC的内接正方形的边长和AC边上的△ABC的内接正方形的边长(不必写出过程,只要直接写出答案即可,结果精确到1mm);
(4)结合第(1)、(3)题,若三角形的三边长分别为a,b,c,各边上的高分别为ha,hb,hc,要使a边上的三角形内接正方形的面积最大,请写出a与ha必须满足的条件(不必写出过程). 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com