
题目列表(包括答案和解析)
导析:由等腰三角形的性质知∠ADB=90°,要证AF⊥BE,只需证∠1=∠2,即证△AFD∽△BEC.易知∠ADF=∠BCE,下面只要证明![]() ,这是解决本题的关键.
,这是解决本题的关键.

如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.

(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状.(只写结果)
如图,在△ABC中,AB=AC,AD⊥BC于D,AE是∠BAC的外角平分线,DE∥AB交AE于E.

求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)
求证:四边形ADCE为矩形;(2)
当△ABC满足什么条件时,四边形ADCE是正方形?并给出证明。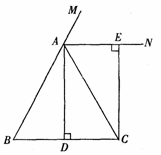
如图,在△
ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.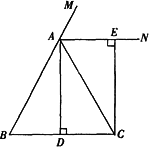
(1)试说明四边形ADCE是矩形.
(2)当△ABC满足什么条件时,四边形ADCE是正方形?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com