
题目列表(包括答案和解析)
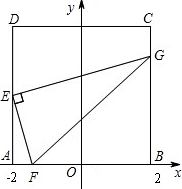 形ABCD,点E 是AD边的中点,F 是x轴上一动点,连接EF,过点E作EG⊥EF,交BC所在的直线与点G,连接FG.
形ABCD,点E 是AD边的中点,F 是x轴上一动点,连接EF,过点E作EG⊥EF,交BC所在的直线与点G,连接FG.| EF |
| EG |
| 1 |
| 2 |
| EF |
| EG |
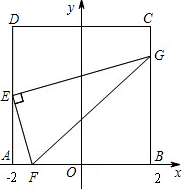 形ABCD,点E 是AD边的中点,F 是x轴上一动点,连接EF,过点E作EG⊥EF,交BC所在的直线与点G,连接FG.
形ABCD,点E 是AD边的中点,F 是x轴上一动点,连接EF,过点E作EG⊥EF,交BC所在的直线与点G,连接FG.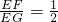 ;若点F与点A不重合时,试问
;若点F与点A不重合时,试问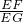 的值是否改变?直接写出正确判断;
的值是否改变?直接写出正确判断;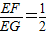 ;若点F与点A不重合时,试问
;若点F与点A不重合时,试问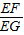 的值是否改变?直接写出正确判断;
的值是否改变?直接写出正确判断;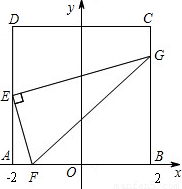
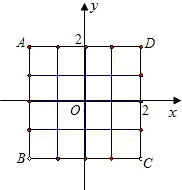
 直线x轴上平移时,正方形ABCD也随之平移,其形状、大小没有改变,当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时,求此时正方形ABCD各顶点的坐标。
直线x轴上平移时,正方形ABCD也随之平移,其形状、大小没有改变,当中心O在x轴上平移到两个正方形公共部分的面积为2个平方单位时,求此时正方形ABCD各顶点的坐标。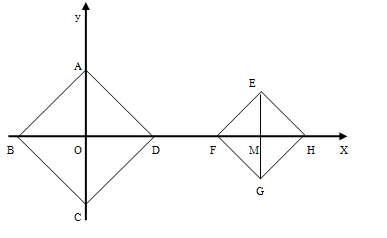
 3,4,5,6,连续抛掷两次,朝上的数字分别作为点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
3,4,5,6,连续抛掷两次,朝上的数字分别作为点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).| 5 | 12 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com