
题目列表(包括答案和解析)
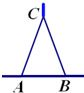
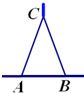 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-| x | 2 |

)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【小题1】求正中间系杆OC的长度;
【小题2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.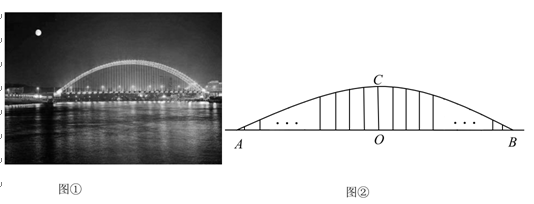
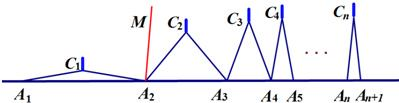
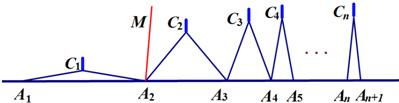
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规。当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-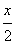 )°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
)°请运用上述知识解决问题: 如图,n个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…
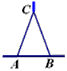
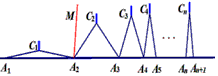
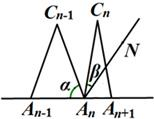
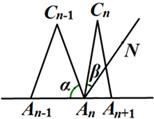
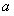 ,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为
,∠An+1AnCn-1的角平分线AnM与AnCn构成的角的度数为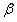 ,那么
,那么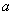 与
与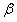 之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图)
之间的等量关系是__________,请说明理由。(提示:可以借助下面的局部示意图) 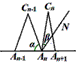
 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90- )°.
)°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com