
题目列表(包括答案和解析)
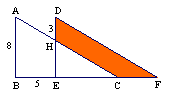
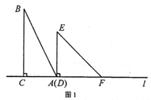
有两个直角三角形,在△ABC中,∠ACB=90°,AC=3,BC=6,在△DEF中,∠FDE=90°,DE=DF=4。将这两个直角三角形按图1所示位置摆放,其中直角边 在同一直线
在同一直线 上,且点
上,且点 与点
与点 重合。现固定
重合。现固定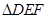 ,将
,将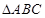 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在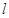 上向右平移,当点
上向右平移,当点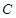 与点
与点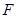 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为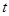 秒。
秒。
(1)当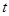 为 秒时,
为 秒时,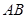 边恰好经过点
边恰好经过点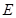 ;当
;当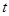 为 秒时,运动停止;
为 秒时,运动停止;
(2)在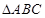 平移过程中,设
平移过程中,设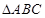 与
与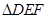 重叠部分的面积为
重叠部分的面积为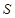 ,请直接写出
,请直接写出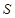 与
与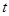 的函数关系式,并写出
的函数关系式,并写出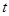 的取值范围;
的取值范围;
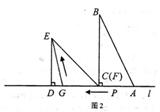
(3)当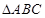 停止运动后,如图2,
停止运动后,如图2,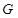 为线段
为线段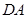 上一点,若一动点
上一点,若一动点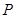 从点
从点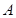 出发,先沿
出发,先沿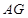 方向运动,到达点
方向运动,到达点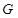 后再沿斜坡
后再沿斜坡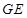 方向运动到达点
方向运动到达点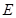 ,若该动点
,若该动点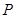 在线段
在线段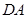 上运动的速度是它在斜坡
上运动的速度是它在斜坡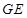 上运动速度的2倍,试确定斜坡
上运动速度的2倍,试确定斜坡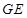 的坡度,使得该动点从点
的坡度,使得该动点从点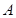 运动到点
运动到点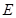 所用的时间最短。(要求,简述确定点
所用的时间最短。(要求,简述确定点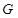 位置的方法,但不要求证明。)
位置的方法,但不要求证明。)
有两个直角三角形,在△ABC中,∠ACB=90°,AC=3,BC=6,在△DEF中,∠FDE=90°,DE=DF=4。将这两个直角三角形按图1所示位置摆放,其中直角边 在同一直线
在同一直线 上,且点
上,且点 与点
与点 重合。现固定
重合。现固定 ,将
,将 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在 上向右平移,当点
上向右平移,当点 与点
与点 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为 秒。
秒。
(1)当 为 秒时,
为 秒时, 边恰好经过点
边恰好经过点 ;当
;当 为 秒时,运动停止;
为 秒时,运动停止;
(2)在 平移过程中,设
平移过程中,设 与
与 重叠部分的面积为
重叠部分的面积为 ,请直接写出
,请直接写出 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)当 停止运动后,如图2,
停止运动后,如图2, 为线段
为线段 上一点,若一动点
上一点,若一动点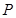 从点
从点 出发,先沿
出发,先沿 方向运动,到达点
方向运动,到达点 后再沿斜坡
后再沿斜坡 方向运动到达点
方向运动到达点 ,若该动点
,若该动点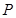 在线段
在线段 上运动的速度是它在斜坡
上运动的速度是它在斜坡 上运动速度的2倍,试确定斜坡
上运动速度的2倍,试确定斜坡 的坡度,使得该动点从点
的坡度,使得该动点从点 运动到点
运动到点 所用的时间最短。(要求,简述确定点
所用的时间最短。(要求,简述确定点 位置的方法,但不要求证明。)
位置的方法,但不要求证明。)
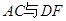 在同一直线
在同一直线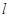 上,且点
上,且点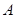 与点
与点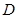 重合。现固定
重合。现固定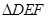 ,将
,将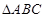 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在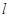 上向右平移,当点
上向右平移,当点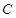 与点
与点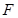 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为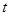 秒。
秒。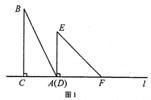
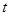 为 秒时,
为 秒时,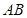 边恰好经过点
边恰好经过点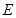 ;当
;当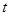 为 秒时,运动停止;
为 秒时,运动停止;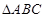 平移过程中,设
平移过程中,设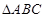 与
与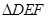 重叠部分的面积为
重叠部分的面积为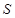 ,请直接写出
,请直接写出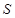 与
与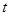 的函数关系式,并写出
的函数关系式,并写出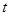 的取值范围;
的取值范围;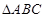 停止运动后,如图2,
停止运动后,如图2,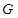 为线段
为线段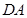 上一点,若一动点
上一点,若一动点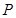 从点
从点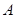 出发,先沿
出发,先沿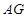 方向运动,到达点
方向运动,到达点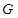 后再沿斜坡
后再沿斜坡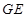 方向运动到达点
方向运动到达点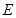 ,若该动点
,若该动点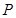 在线段
在线段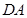 上运动的速度是它在斜坡
上运动的速度是它在斜坡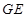 上运动速度的2倍,试确定斜坡
上运动速度的2倍,试确定斜坡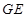 的坡度,使得该动点从点
的坡度,使得该动点从点 运动到点
运动到点 所用的时间最短。(要求,简述确定点
所用的时间最短。(要求,简述确定点 位置的方法,但不要求证明。)
位置的方法,但不要求证明。)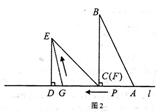
两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED按图1所示的位置放置A与C重合,O与E重合.
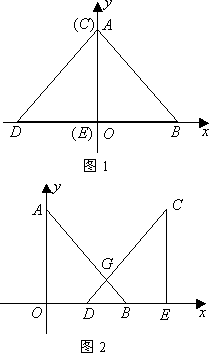
(1)求图1中,A,B,D三点的坐标.
(2)Rt△AOB固定不动,Rt△CED沿x轴以每秒2个单位长的速度向右运动,当D点运动到与B点重合时停止,设运动x秒后Rt△CED和Rt△AOB重叠部分面积为y,求y与x之间的函数关系式.
(3)当Rt△CED以(2)中的速度和方向运动,运动时间x=4秒时RT△CED运动到如图2所示的位置,求经过A,G,C三点的抛物线的解析式.
(4)现有一半径为2,圆心P在(3)中的抛物线上运动的动圆,试问⊙P在运动过程中是否存在⊙P与x轴或y轴相切的情况,若存在请求出P的坐标,若不存在请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com