
题目列表(包括答案和解析)
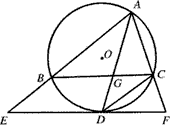
| 如图,在Rt△ABC中,∠BAC=90°,∠C=60°,BC=24,点P是BC边上的动点(点P与点B、C不重合),过动点P作PD∥BA交AC于点D。 (1)若△ABC与△DPA相似,则∠APD是多少度? (2)试问:当PC等于多少时,△APD的面积最大?最大面积是多少? (3)若以线段AC为直径的圆和以线段BP为直径的圆相外切,求线段BP的长。 | |
 |





 周。
周。 c,⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,则⊙O自转____周;
c,⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,则⊙O自转____周;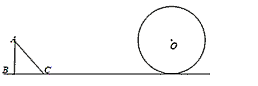
如图1至图4,⊙![]() 均作无滑动滚动,⊙
均作无滑动滚动,⊙![]() 、⊙
、⊙![]() 均表示⊙
均表示⊙![]() 与线段AB、BC或弧AB相切于端点时刻的位置,⊙
与线段AB、BC或弧AB相切于端点时刻的位置,⊙![]() 的周长为
的周长为![]() ,请阅读下列材料:
,请阅读下列材料:
①如图1,⊙![]() 从⊙
从⊙![]() 的位置出发,沿AB滚动到⊙
的位置出发,沿AB滚动到⊙![]() 的位置,当AB=
的位置,当AB=![]() 时,⊙
时,⊙![]() 恰好自转1周。
恰好自转1周。
②如图2,∠ABC相邻的补角是n°, ⊙![]() 在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙
在∠ABC外部沿A-B-C滚动,在点B处,必须由⊙![]() 的位置转到⊙
的位置转到⊙![]() 的位置,⊙
的位置,⊙![]() 绕点B旋转的角∠
绕点B旋转的角∠![]() = n°, ⊙
= n°, ⊙![]() 在点B处自转
在点B处自转![]() 周。
周。

解答以下问题:
⑴在阅读材料的①中,若AB=2![]() ,则⊙
,则⊙![]() 自转 周;若AB=
自转 周;若AB=![]() ,则⊙
,则⊙![]() 自转 周。在阅读材料的②中,若∠ABC=120°,则⊙
自转 周。在阅读材料的②中,若∠ABC=120°,则⊙![]() 在点B处自转 周;
在点B处自转 周;
若∠ABC=60°,则⊙![]() 在点B处自转 周。
在点B处自转 周。
⑵如图13-3,△ABC的周长为![]() ,⊙
,⊙![]() 从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙
从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙![]() 自转多少周?
自转多少周?
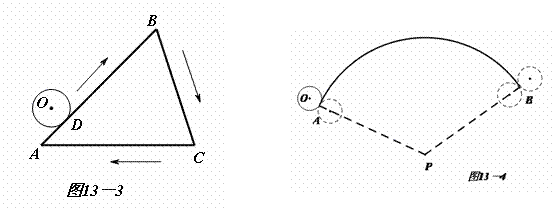 |
⑶如图13-4,半径为2的⊙![]() 从半径为18,圆心角为120°的弧的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙
从半径为18,圆心角为120°的弧的一个端点A(切点)开始先在外侧滚动到另一个端点B(切点),再旋转到内侧继续滚动,最后转回到初始位置,⊙![]() 自转多少周?
自转多少周?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com