
题目列表(包括答案和解析)
 分别画出这两个函数的图象
分别画出这两个函数的图象 的面积
的面积(本题10分)已知一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q(0,4)
【小题1】(1)求这两个函数的解析式
【小题2】(2)在同一坐标系内, 分别画出这两个函数的图象
分别画出这两个函数的图象
【小题3】(3)求出 的面积
的面积
 的面积
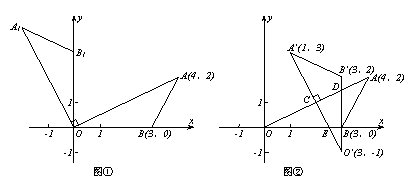
的面积课堂上,老师将图①中△AOB绕O点逆时针旋转,在旋转中发现图形的形状和大小不变,但位置发生了变化.当△AOB旋转90°时,得到△A1OB1.已知A(4,2)、B(3,0).
(1)△A1OB1的面积是 ;A1点的坐标为( , );B1点的坐标为( , );
(2)课后,小玲和小惠对该问题继续进行探究,将图②中△AOB绕AO的中点C(2,1)逆时针旋转90°得到△A’O’B’,设O’B’交OA于点D,O’A’交x轴于E.此时A’、O’和B’的坐标分别为(1,3)、(3,-1)和(3,2),且O’B’经过B点.在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CEBD的面积。 (本题10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com