
题目列表(包括答案和解析)
直接写出因式分解的结果:
(1)x2y2-y2=___________;
(2)3a2-6a+3=__________.
(1)-![]() x2+0.04;
x2+0.04;
(2)16a2b4-8ab3c2+b2c4;
(3)![]() ;
;
(4)y(x-y)-![]() x2;
x2;
(5)16x5-49xy4;
(6)7am+1-14am+7am-1;
(7)(3a2-b2)2-(a2-3b2)2;
(8)2(x2+y2)(x+y)2-(x2-y2)2.
对于形如x2+2ax+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式。但对于二次三项式x2+2ax-3a2,就不能直接运用公式了。此时,我们可以在二次三项式x2+2ax-3a2中先加上一项a2,使它与x2+2ax的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:
x2+2ax-3a2= (x2+2ax+a2)-a2-3a2
=(x+a)2-(2a)2
=(x+3a)(x-a).
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”。
(1)利用“配方法”分解因式:a2-4a+3;(4分)
(2)若a+b=5,ab=6,求:a2+b2的值。 (3分)
通过本节课的学习,我们已经会对某些形如x2+px+q型二次三项式进行因式分解,此类多项式的特点是二次项的系数为1,如二次项的系数不为1,比如多项式3x2+11x+10又如何分解呢?
我们知道(x+2)(3x+5)=3x2+11x+10.反过来,就得到3x2+11x+10的因式分解的形式,即3x2+11x+10=(x+2)(3x+5).
我们发现,二次项的系数3分解成1、3两个因数的积;常数项10分解成2、5两个因数的积;当我们把1、3、2、5写成
1
![]()
![]() 2
2
3 5
后发现1×5+2×3恰好等于一次项的系数11.
像这种借助画十字交叉线分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做十字相乘法.
请用十字相乘法将下列各式分解因式:
(1)2x2-7x+3; (2)3a2-8a+4;
(3)6y2-11y-10; (4)5a2b2+23ab-10.
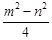 ;
;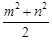
| A.1个 | B.2个 | C.3个 | D.4个 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com