
题目列表(包括答案和解析)
(本题满分10分) 把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,
∠CAB=45°,∠CDE=30°,且AB=12,DC=14,把△DCE绕点C顺时针旋转15°
得△D1CE1,如图2,这时AB与CD1相交于点O、与D1E1相交于点F;
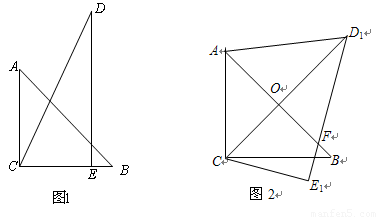
1.(1)求∠AC D1的度数;
2.(2)求线段AD1的长.

(本题满分10分) 把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,
∠CAB=45°,∠CDE=30°,且AB=12,DC=14,把△DCE绕点C顺时针旋转15°
得△D1CE1,如图2,这时AB与CD1相交于点O、与D1E1相交于点F;
【小题1】(1)求∠AC D1的度数;
【小题2】(2)求线段AD1的长.
(本题满分10分) 把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,
∠CAB=45°,∠CDE=30°,且AB=12,DC=14,把△DCE绕点C顺时针旋转15°
得△D1CE1,如图2,这时AB与CD1相交于点O、与D1E1相交于点F;
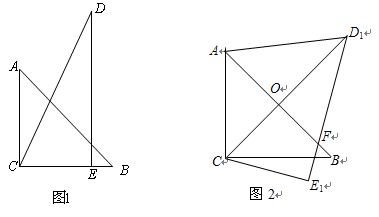
1.(1)求∠AC D1的度数;
2.(2)求线段AD1的长.
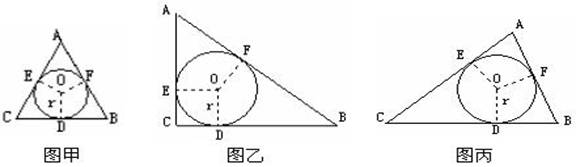
(本题满分12分)为了探究三角形的内切圆半径r与周长![]() 、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长![]() 和面积S.(结果精确到0.1厘米)
和面积S.(结果精确到0.1厘米)
|
| AC | BC | AB | r |
| S |
| 图甲 |
|
|
| 0.6 |
|
|
| 图乙 |
|
|
| 1.0 |
|
|
(2)观察图形,利用上表实验数据分析.猜测特殊三角形的r与![]() 、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
(3) 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com