
题目列表(包括答案和解析)
设 是
是 函数的两个极值点.
函数的两个极值点.
(1)试确定常数 和
和 的值;
的值;
(2)试判断 是函数
是函数 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.
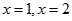 是
是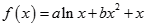 函数的两个极值点.
函数的两个极值点.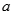 和
和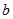 的值;
的值;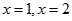 是函数
是函数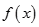 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.| 1 |
| 3 |
| 2 |
| 2 |
设函数 ,其中
,其中 为常数.
为常数.
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)当 时,求
时,求 的极值点并判断是极大值还是极小值;
的极值点并判断是极大值还是极小值;
(Ⅲ)求证对任意不小于3的正整数 ,不等式
,不等式 都成立.
都成立.
设函数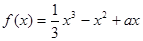 ,
,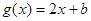 ,当
,当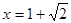 时,
时,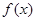 取得极值。
取得极值。
⑴求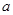 的值,并判断
的值,并判断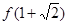 是函数
是函数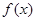 的极大值还是极小值;
的极大值还是极小值;
⑵当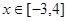 时,函数
时,函数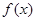 与
与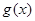 的图象有两个公共点,求
的图象有两个公共点,求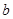 的取值范围。
的取值范围。
一. 选择题 : (本大题共10小题, 每小题5分, 共50分)
ABDCC DDBCB
二.填空题: (本大题共5小题, 每小题5分, 共25分)
11.1680 12.5
13.-1 14. 15.
15.
三. 解答题: (本大题共6小题, 共75分)
16.(本小题满分12分)
解:(1)f(x)

 ......3分
......3分
 ……4分
……4分
令

 的单调区间为
的单调区间为 ,k∈Z ...............6分
,k∈Z ...............6分
(2)由 得
得
 ......7分
......7分
又 为
为 的内角
的内角 

 .....9分
.....9分


 .......11分
.......11分

 ......12分
......12分
17.(本小题满分12分)
解:(1) .......5分
.......5分
 .......12分
.......12分
18.(本题满分12分)
解法一:
(1)在棱 取三等分点
取三等分点 ,使
,使 ,则
,则 ,由
,由 ⊥平面
⊥平面 ,
,
得 ⊥平面
⊥平面 。过点
。过点 作
作 于
于 ,连结
,连结 ,
,
 则
则 ,
, 为所求二面角
为所求二面角 的平面角.
的平面角.
在 中,
中, ,
,
 ,
,
 所以,二面角
所以,二面角 的余弦值为
的余弦值为 ......6分
......6分
(2)因为 ,所以点
,所以点 到平面
到平面 的距离等于
的距离等于
 到平面
到平面 的距离,
的距离, ⊥平面
⊥平面 ,
,
过点 作
作 于
于 ,连结
,连结 ,则
,则 ,
,
 ⊥平面
⊥平面 ,过点
,过点 作
作 于
于 ,
,
则 ,
, 为所求距离,
为所求距离,


所以,求点 到平面
到平面 的距离为
的距离为 ......12分
......12分
解法二:
证明:(1)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,3,0)、P(0,0,3)、
B(4,0,0)、C(4,3,0), 由已知得 ,
,
得 .
.
设平面QAC的法向量为 ,则
,则 ,
,
即 ∴
∴ ,令
,令 ,得到平面QAC的一个法向量为
,得到平面QAC的一个法向量为
∵PA⊥平面ABCD,∴ 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P―CD―B的大小为q,依题意可得 .....6分
.....6分
(2)由(1)得
设平面PBD的法向量为 ,则
,则 ,
,
即 ,∴令
,∴令 ,得到平面QAC的一个为法向量为
,得到平面QAC的一个为法向量为
19. (本小题满分13分)
(1)解:当
 时,
时, ,………………………………①
,………………………………①
则当 ,
, 
 时,
时, ………………②
………………②
①-②,得 ,即
,即
∴ ,∴
,∴ ,当
,当 时,
时, ,则
,则 .
.
∴ 是以
是以 为首项,
为首项, 为公比的等比数列,∴
为公比的等比数列,∴ ,
,
∴ ………………………6分
………………………6分
(2)证明: .
.
∴ , 则
, 则 ,…………③
,…………③
 …………………………④
…………………………④
③-④,得


 ∴
∴ .
.
当 时,
时, , ∴
, ∴ 为递增数列,
为递增数列,
∴ ........13分
........13分
 20.(本小题满分13分)
20.(本小题满分13分)
解法一:
(1)设椭圆方程为 (a>b>0),由已知c=1,
(a>b>0),由已知c=1,
又 .
.
所以a= ,b2=a2-c2=1,
,b2=a2-c2=1,
椭圆C的方程是x2+  =1. .......4分
=1. .......4分
(2)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1,
若直线l垂直于x轴,则以AB为直径的圆是(x+ )2+y2=
)2+y2= .
.
由 解得
解得 即两圆相切于点(1,0).
即两圆相切于点(1,0).
因此所求的点T如果存在,只能是(1,0). 事实上,点T(1,0)就是所求的点........6分
证明如下:
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).
若直线l不垂直于x轴,可设直线l:y=k(x+ ).
).
由 即(k2+2)x2+
即(k2+2)x2+ k2x+
k2x+ k2-2=0.记点A(x1,y1),B(x2,y2),则
k2-2=0.记点A(x1,y1),B(x2,y2),则
由 =(x1-1, y1),
=(x1-1, y1),  =(x2-1, y2),
=(x2-1, y2),  =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+ )(x2+
)(x2+ )
)
=(k2+1)x1x2+( k2-1)(x1+x2)+
k2-1)(x1+x2)+ k2+1=(k2+1)
k2+1=(k2+1)  +(
+( k2-1)
k2-1)  +
+  +1=0,
+1=0,
所以TA⊥TB,即以AB为直径的圆恒过点T(1,0).故在坐标平面上存在一个定点T(1,0)满足条件.......13分
解法二:
(1)由已知c=1,设椭圆C的方程是 (a>1).
(a>1).
因为点P在椭圆C上,所以 ,解得a2=2,所以椭圆C的方程是:
,解得a2=2,所以椭圆C的方程是: .
.
.......4分
(2)假设存在定点T(u,v)满足条件.同解法一得(k2+2)x2+ k2x+
k2x+ k2-2=0.
k2-2=0.
记点A(x1,y1),B(x2,y2),则
又因为 =(x1-u, y1-v),
=(x1-u, y1-v),  =(x2-u, y2-v),及y1=k(x1+
=(x2-u, y2-v),及y1=k(x1+ ),y2=k(x2+
),y2=k(x2+ ).
).
所以 =(x1-u)(x2-u)+(y1-v)(y2-v)
=(x1-u)(x2-u)+(y1-v)(y2-v)
=(k2+1)x1x2+( k2-u-kv)(x1+x2)+
k2-u-kv)(x1+x2)+ k2-
k2- v+u2+v2
v+u2+v2
=
当且仅当 ?
? =0恒成立时,以AB为直径的圆恒过点T.
=0恒成立时,以AB为直径的圆恒过点T.
 ?
? =0恒成立等价于
=0恒成立等价于 解得u=1,v=0.
解得u=1,v=0.
此时,以AB为直径的圆恒过定点T(1,0). 当直线l垂直于x轴时,以AB为直径的圆 亦过点T(1,0).所以在坐标平面上存在一个定点T(1,O)满足条件
亦过点T(1,0).所以在坐标平面上存在一个定点T(1,O)满足条件
........13分
解法三:
(1)同解法一或解法二........4分
(2)设坐标平面上存在一个定点T满足条件,根据直线过x轴上的定点S及椭圆的对称性,所求的点T如果存在,只能在x轴上,设T(t,O).
同解法一得

 =(x1-t,y1),
=(x1-t,y1), =(x2-t,y2)
=(x2-t,y2)

 =(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+
=(x1-t)(x2-t)+y1y2=(x1-t)(x2-t)+k2(x1+ )(x2+
)(x2+ )
)
=(k2+1)x1x2+( k2-t)(x1+x2)+
k2-t)(x1+x2)+ k2+t2=
k2+t2=
当且仅当 ?
? =O恒成立时,以AB为直径的圆恒过点T.
=O恒成立时,以AB为直径的圆恒过点T.
 ?
? =O恒成立等价于
=O恒成立等价于 解得t=1.所以当t=1时,以AB为直径的圆恒过点T.
解得t=1.所以当t=1时,以AB为直径的圆恒过点T.
当直线l垂直于x轴时,以AB为直径的圆 亦过点T(1,O).
亦过点T(1,O).
所以在坐标平面上存在一个定点T(1,O)满足条件........13分
21. (本小题满分13分)
解:(1)由题意
 …………………………1分
…………………………1分
 当
当 时,
时, 取得极值,
取得极值,  所以
所以 

 即
即  …………………3分
…………………3分
此时当 时,
时, ,当
,当 时,
时, ,
,
 是函数
是函数 的最小值。 ………………………5分
的最小值。 ………………………5分
(2)设 ,则
,则  ,
, ……8分
……8分
设 ,
,
 ,令
,令 解得
解得 或
或
列表如下:











__
0
+










 函数
函数 在
在 和
和 上是增函数,在
上是增函数,在 上是减函数。
上是减函数。
当 时,
时, 有极大值
有极大值 ;当
;当 时,
时, 有极小值
有极小值 ……10分
……10分
 函数
函数 与
与 的图象有两个公共点,
的图象有两个公共点, 函数
函数 与
与 的图象有两个公共点
的图象有两个公共点
 或
或 
 ……13分
……13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com