小明在做作业时,不慎将墨水滴在一个三项式上,将前后两项污染得看不清楚了,但中间项是12xy,为了便于填上后面的空,请你帮他把前后两项补充完整,使它成为完全平方式,你有几种方法?(至少写出三种不同的方法)
三项式:■+12xy+■=______2.
(1)______;(2)______;(3)______.
我们知道因式分解与整式乘法是互逆的关系,那么逆用乘法公式(x+a)(x+b)=x2+(a+b)x+ab,即x2+(a+b)x+ab=(x+a)(x+b)是否可以分解因式呢?当然可以,而且也很简单.
如:
(1)x2+5x+6=x2+(3+2)x+3×2=(x+2)(x+3);
(2)x2-5x-6=x2+(-6+1)x+(-6)×1=(x-6)(x+1).
请你仿照上述方法,把下列多项式分解因式:
(1)x2-8x+7;
(2)x2+7x-18.

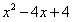 ;②
;②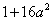 ;③
;③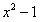 ;④
;④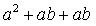 ;⑤
;⑤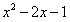 ;⑥
;⑥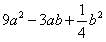 中,是完全平方式的有
中,是完全平方式的有