
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 7 |
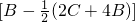 ,再求当x=
,再求当x= 时的此式的值.
时的此式的值.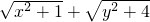 的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2.
的最小值.分析:(1)如图(1),作长为6的线段AB,过A、B两点在同侧各做AC⊥AB,BD⊥AB,使AC=1,BD=2. ,PD=
,PD=

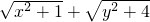 的最小值.问题:①在图(2)中作出符合上述要求的点.
的最小值.问题:①在图(2)中作出符合上述要求的点.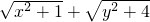 的最小值为________.
的最小值为________.
 阅读材料:
阅读材料: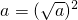 .如:2=
.如:2= ,
,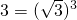 等.
等.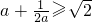 .
.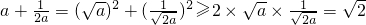
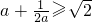 ,当且仅当
,当且仅当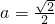 时,等号成立.
时,等号成立. .如:2=
.如:2= ,
, 等.
等. .
.
 ,当且仅当
,当且仅当 时,等号成立.
时,等号成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com