
题目列表(包括答案和解析)
如图,一次函数的图象与反比例函数y1=- (x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值
(x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值

1.求一次函数的解析式
2.设函数y2= (x>0)的图象与y1=-
(x>0)的图象与y1=- (x<0)的图象关于y轴对称,在y2=
(x<0)的图象关于y轴对称,在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
(x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
 的图象经过点 P(-2,5).
的图象经过点 P(-2,5).  在这个二次函数的图象上.
在这个二次函数的图象上. 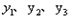 能否作为同一个三角形的三边的长?请说明理由
能否作为同一个三角形的三边的长?请说明理由  一定能作为同一个三角形三边的长,请说明理由.
一定能作为同一个三角形三边的长,请说明理由.如图,在平面直角坐标系xoy中,抛物线y=![]() x 2-
x 2-![]() x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)

(1)求A,C两点的坐标和抛物线的顶点M坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<4.5时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
如图,在平面直角坐标系xoy中,抛物线y= x 2-
x 2- x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)

(1)求A,C两点的坐标和抛物线的顶点M坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当0<t<4.5时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
永定土楼是世界文化遗产“福建土楼”的组成部分,是闽西的旅游胜地. “永定土楼”模型深受游客喜爱.其中某种规格土楼模型的单价y(元)与购买数量x(个)之间的函数关系如下:当0<x≤10时,y=200;当10<x<20时,y=-5x+250;当x≥20时,y=150。

(1)若甲旅游团购买该种规格的土楼模型10个,则一共需要 元;若乙旅游团购买该种规格的土楼模型20个,则一共需要 元。
(2)某旅游团购买该种规格的土楼模型总金额为2625元,问该旅游团共购买这种土楼模型多少个?(总金额=数量×单价)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com