
题目列表(包括答案和解析)
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 | 频数 | 百分比 |
|
| 2 | 5% |
| 800 | 6 | 15% |
| 1000 |
| 45% |
|
| 9 | 22.5% |
|
|
|
|
| 1600 | 2 |
|
| 合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
(本小题满分10分)
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.
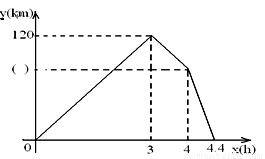
1.(1)将图中( )填上适当的值,并求甲车从A到B的速度.
2.(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,自变量取值范围。
3.(3) 求出甲车返回时行驶速度及AB两地的距离.
(本小题满分10分)
如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.
思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.
探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.
探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.
⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:
⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() )
)
(2011广西崇左,22,10分)(本小题满分10分)矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的_______相等;或者先证明四边形是菱形,在证明这个菱形有一个角是________ .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2,对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明.
(本小题满分10分)
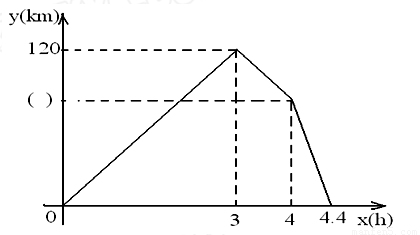
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.
(1)将图中( )填上适当的值,并求甲车从A到B的速度.
(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,自变量取值范围。
(3) 求出甲车返回时行驶速度及AB两地的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com