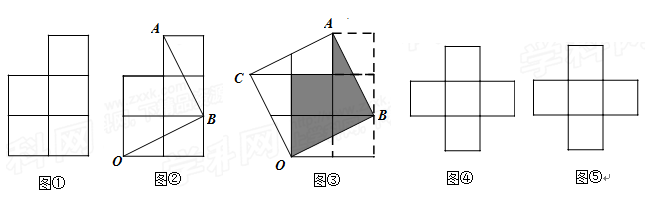
解：（1）旋转后的图象解析式为．  ………………………  1分

（2）由旋转可得（4，-1）、（1，-4）．  …………………………  3分

（3）依题意，可知．若为直角三角形，则同时也是等腰三角形，因此，只需求使为直角三角形的值．

分两种情况讨论：

①当是直角，时，如图1，

∵AB′=8，B′A′==，AM=B′N=MN=t，

∴B′M=8-t，

∵，

∴．  …………  4分

解得  （舍去负值），

∴．  ………………  5分

②当是直角，时，

如图2，

∵AB′=8，B′A′==，AM=B′N=t，

∴B′M=MN=8-t，

∵，

∴，

解得  ．

∵，，

∴此时t值不存在．  ……………  6分

（此类情况不计算，通过画图说明t值不存在也可以）

综上所述，当时，为等腰直角三角形．  ………………  7分

以Rt△OAB的两直角边所在的直线为轴，以直角顶点O为原点，建立直角坐标系. 如图所示，且点A、B的坐标分别为（0，8）和（6，0）．若保持线段AB的长度不变，点A在y轴正半轴上向下滑动，则点B在x轴正半轴上向右滑动．

（1）求Rt△OAB斜边AB上的高h的长度．

（2）如果点A下滑1个单位长度到点C，则点B向右滑动到点D，猜一猜点B滑动的距离比1大，还是比1小，或者等于1？设BD=x, 列出点B滑动距离x满足的方程，并尝试得出这个方程的近似解．（保留一位小数）

（3）是否存在点A和点B滑动距离相等的情形？若存在，试求出此时三角形与原Rt△OAB的公共部分面积，若不存在，请说明理由．