
题目列表(包括答案和解析)
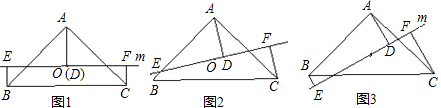
 为等腰直角三角形
为等腰直角三角形 的重心,
的重心, ,直线
,直线 过点
过点 ,过
,过 三点分别作直线
三点分别作直线 的垂线,垂足分别为点
的垂线,垂足分别为点 .
.  与
与 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段 和
和 三者之间的数量关系并证明;
三者之间的数量关系并证明; 绕点
绕点 旋转到与
旋转到与 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段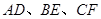 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.
我们知道三角形三条中线的交点叫做三角形的重心.经过证明我们可得三角形重心具备下面的性质: 重心到顶点的距离与重心到该顶点对边中点的距离之比为2﹕1.请你用此性质解决下面的问题.
已知:如图,点 为等腰直角三角形
为等腰直角三角形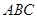 的重心,
的重心, ,直线
,直线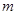 过点
过点 ,过
,过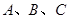 三点分别作直线
三点分别作直线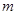 的垂线,垂足分别为点
的垂线,垂足分别为点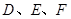 .
.
<1>当直线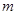 与
与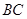 平行时(图1),请你猜想线段
平行时(图1),请你猜想线段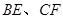 和
和 三者之间的数量关系并证明;
三者之间的数量关系并证明;
<2>当直线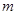 绕点
绕点 旋转到与
旋转到与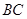 不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段
不平行时,分别探究在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段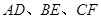 三者之间又有怎样的数量关系?请写出你的结论,不需证明.
三者之间又有怎样的数量关系?请写出你的结论,不需证明.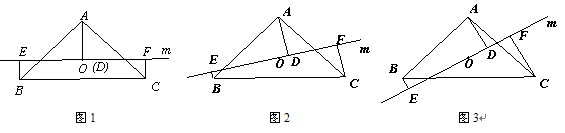

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com