
题目列表(包括答案和解析)
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边长作正方形PQMN,使点M落在反比例函数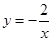 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点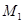 在第二象限;
在第二象限;
(1)如图所示,点P坐标为(1,0),图中已画出一个符合条件的正方形PQMN,请你在图中画出符合条件的另一个正方形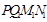 ,并写出点
,并写出点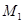 的坐标;
的坐标;
(2)请你通过改变P点的坐标,对直线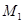 M的解析式y﹦kx+b进行探究:
M的解析式y﹦kx+b进行探究:
①k= ;
②若点P的坐标为(m,0),则b= ;
(3)依据(2)的规律,如果点P的坐标为(8,0),请你求出点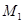 和点M的坐标.
和点M的坐标.
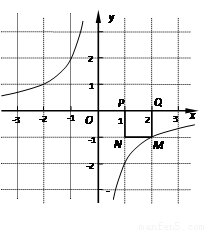
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边长作正方形PQMN,使点M落在反比例函数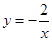 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点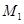 在第二象限;
在第二象限;
(1)如图所示,点P坐标为(1,0),图中已画出一个符合条件的正方形PQMN,请你在图中画出符合条件的另一个正方形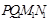 ,并写出点
,并写出点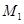 的坐标;
的坐标;
(2)请你通过改变P点的坐标,对直线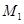 M的解析式y﹦kx+b进行探究:
M的解析式y﹦kx+b进行探究:
①k= ;
②若点P的坐标为(m,0),则b= ;
(3)依据(2)的规律,如果点P的坐标为(8,0),请你求出点 和点M的坐标.
和点M的坐标.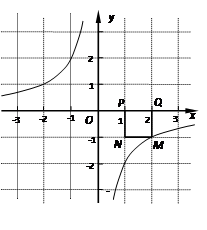
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边长作正方形PQMN,使点M落在反比例函数![]() 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点![]() 在第二象限;
在第二象限;
(1) 如图7所示,点P坐标为(1,0),图中已画出一个符合条件的正方形PQMN,请你在图中画出符合条件的另一个正方形![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2) 请你通过改变P点的坐标,对直线![]() M的解析式y﹦kx+b进行探究:
M的解析式y﹦kx+b进行探究:
①写出k的值;
②若点P的坐标为(m,0),求b的值;
(3) 依据(2)的规律,如果点P的坐标为(8,0),请你求出点![]() 和点M的坐标.
和点M的坐标.
 |
| k | x |
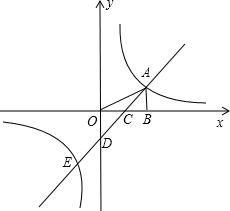 如图,在平面直角坐标系中,点A是反比例函数y1=
如图,在平面直角坐标系中,点A是反比例函数y1=| k |
| x |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com