2010年8月31日,全国绿化委员会、国家林业局、重庆市人民政府共同发起“绿化长江重庆行动”,该行动就是要加快长江两岸造林绿化步伐,保护母亲河,促进入与自然和谐共生.某园艺公司从 9 月开始积极响应这一行动,进行植树造林.该公司第 x 月种植树木的亩数 y(亩)与 x 之间满足y=x+4,(其中x从9月算起,即9月时 x=l,10月时x=2,…,且1≤x≤6,x为正整数).但由于植树规模增加,每亩的收益会相应降低,每亩的收益 P(千元)与种植树木亩数 y(亩)之间的关系如下表:
| 亩数y(亩) |
5 |
6 |
7 |
8 |
… |
| 每亩收益P(千元/亩) |
46 |
44 |
42 |
40 |
… |
(1)请观察题中的表格,用所学过的一次函数、二次函数和反比例函数的有关知识求出 P与 y 之间所 满足的函数关系表达式:
(2)求该行动实施六个月来,第几月的总收益最大?此时每亩收益为多少?
(3)进入三月份,便是植树造林的“黄金期”,为此政府出台了一项激励措施:在“植树造林”过程中,每月植树面积与二月份植树面积相同的部分,按二月份每亩收益进行结算;超出二月份植树面积 的部分,每亩收益将按二月份时每亩的收益再增加 0.6a%进行结算.这样,该公司三月份植树面积比二月份的植树面积增加了a%.另外,三月份时公司需对三月份之前种植的所有树木进行保养,除去成本后政府给予每亩 5a%千元的保养补贴.最后,该公司三月份获得种植树木的收益和政府保养补贴共 702 千元.请通过计算,估算出 a 的整数值.
(参考数据:87
2=7569,88
2=7744,89
2=7921,90
2=8100)

 【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)
【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)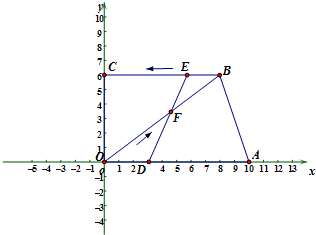 如图,在平面直角坐标系中,点A(10,0),点C(0,6),BC∥OA,OB=10,点E从点B出发,以每秒1个单位长度沿BC向点C运动,点F从点O出发,以每秒2个单位长度沿OB向点B运动,现点E、F同时出发,连接EF并延长交OA于点D,当F点到达B点时,E、F两点同时停止运动.设运动时间为t秒
如图,在平面直角坐标系中,点A(10,0),点C(0,6),BC∥OA,OB=10,点E从点B出发,以每秒1个单位长度沿BC向点C运动,点F从点O出发,以每秒2个单位长度沿OB向点B运动,现点E、F同时出发,连接EF并延长交OA于点D,当F点到达B点时,E、F两点同时停止运动.设运动时间为t秒 点E、F运动的时间t的值;如果不会,请说明理由.
点E、F运动的时间t的值;如果不会,请说明理由.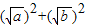 =
=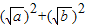 -
-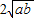 +
+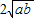 =
=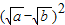 +
+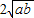 ,
,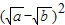 ≥0,∴
≥0,∴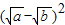 +
+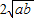 ≥0+
≥0+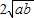 ,即a+b≥
,即a+b≥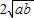 .
.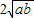 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥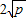 ,当且仅当a、b满足______时,a+b有最小值
,当且仅当a、b满足______时,a+b有最小值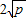 .
.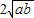 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.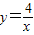 的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.
的图象上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连接DF、EF,求四边形ADFE面积的最小值.