
题目列表(包括答案和解析)
| 1 |
| 2 |
| 5-8x |
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴.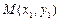 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程; 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.请阅读下面材料:
若![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
∴  且
且 ![]() ≠
≠![]() .
.
①-②得 ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
又∵ 抛物线![]() (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为![]() ,
,
∴ 直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
(1)反之,如果![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的
(a ≠ 0)上不同的
两点,直线![]() 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取![]() ,
,![]() 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
(2)利用以上结论解答下面问题:
已知二次函数![]() 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
, 为此抛物线的对称轴.
为此抛物线的对称轴.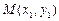 ,
,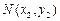 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程; 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值. 三峡工程在2003年6月1日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡出平湖初现人间.如图是三峡水库水位变化图象,其中x表示下闸蓄水时间(天),y表示水库的平均水位(米).根据图象回答下列问题:
三峡工程在2003年6月1日至6月10日下闸蓄水期间,水库水位由106米升至135米,高峡出平湖初现人间.如图是三峡水库水位变化图象,其中x表示下闸蓄水时间(天),y表示水库的平均水位(米).根据图象回答下列问题:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com