(1)夜晚,小明在路灯下散步.已知小明身高1.5米,路灯的灯柱高4.5米.
①如图1,若小明在相距10米的两路灯AB、CD之间行走(不含两端),他前后的两个影子长分别为FM=x米,FN=y米,试求y与x之间的函数关系式,并指出自变量x的取值范围?
②有言道:形影不离.其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图2,若小明在灯柱PQ前,朝着影子的方向(如图箭头),以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
(2)我们知道,函数图象能直观地刻画因变量与自变量之间的变化关系.相信,大家都听说过龟兔赛跑的故事吧.现有一新版龟兔赛跑的故事:由于兔子上次比赛过后不服气,于是单挑乌龟再来另一场比赛,不过这次路线由乌龟确定…比赛开始,在同一起点出发,按照规定路线,兔子飞驰而出,极速奔跑,直至跑到一条小河边,遥望着河对岸的终点,兔子呆坐在那里,一时不知怎么办.过了许久,乌龟一路跚跚而来,跳入河中,以比在陆地上更快的速度游到对岸,抵达终点,再次获胜.根据新版龟兔赛跑的故事情节,请在同一坐标系内(如图3),画出乌龟、兔子离开终点的距离s与出发时间t的函数图象示意图.(实线表示乌龟,虚线表示兔子)

 ?若存在,求出BP的长;若不存在,说明理由.
?若存在,求出BP的长;若不存在,说明理由.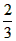 ,若存在,求出BP的长,若不存在,说明理由。
,若存在,求出BP的长,若不存在,说明理由。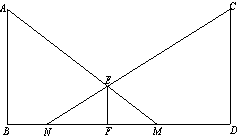 (图一)
(图一)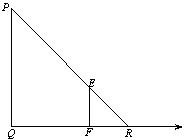 (图二)
(图二) (图三)
(图三)