
题目列表(包括答案和解析)
请写出一个式子,使它与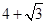 的积不含二次根式
的积不含二次根式
(本题8分)已知二次函数y=- x2+bx+c的图象经过A(2,0),B(0,-6)两点
x2+bx+c的图象经过A(2,0),B(0,-6)两点

(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积和周长.
请写出一个式子,使它与![]() 的积不含二次根式
的积不含二次根式
 的积不含二次根式
的积不含二次根式  ,
, ,
,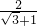 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: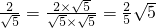 ;(一)
;(一) =
=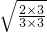 =
= ;(二)
;(二)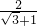 =
=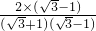 =
=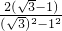 =
= -1 (三)
-1 (三)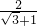 还可以用以下方法化简:
还可以用以下方法化简: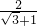 =
=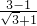 =
=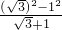 =
=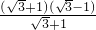 =
= -1(四)
-1(四)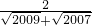 (2).
(2).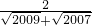 ;
;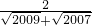 .
.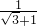 +
+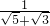 +
+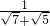 +…+
+…+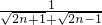 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com