
题目列表(包括答案和解析)
已知函数![]() ,
,![]() 。
。
(Ⅰ)求![]() 在区间
在区间![]() 的最小值;
的最小值;
(Ⅱ)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立;
恒成立;
(Ⅲ)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意
对于任意![]() 的
的![]()
![]() 恒成立。
恒成立。
已知函数![]() 在区间[m,n]上为增函数,
在区间[m,n]上为增函数,
(Ⅰ)若m=0,n=1时,求实数a的取值范围;
(Ⅱ)若f(m)f(n)=-4.则当f(n)-f(m)取最小值时,
(ⅰ)求实数a的值;
(ⅱ)若P(x1,y1),Q(x2,y2)(a<x1<x2<n)是f(x)图象上的两点,且存在实数x0=(a,n)使得![]() ,证明:x1<x0<x2.
,证明:x1<x0<x2.
| x+1 |
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
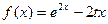 ,
,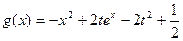 。
。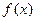 在区间
在区间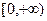 的最小值;
的最小值;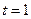 ,则不等式
,则不等式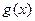 ≥
≥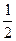 对于任意的
对于任意的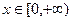 恒成立;
恒成立;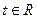 ,则不等式
,则不等式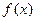 ≥
≥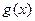 对于任意
对于任意 的
的
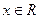 恒成立。
恒成立。(本小题满分12分)已知函数![]() ,
,![]() .
.
(1)求![]() 在区间
在区间![]() 的最小值; (2)求证:若
的最小值; (2)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立; (3)求证:若
恒成立; (3)求证:若![]() ,则不等式
,则不等式![]() ≥
≥![]() 对于任意的
对于任意的![]() 恒成立.
恒成立.
一、选择题:本大题共10小题,每小题5分,共50分.
CBCDB DADCA
二、填空题:本大题共5小题,每小题5分,共25分.
11.90 12.[ ) 13.
) 13. 14.1 ;3899 15.
14.1 ;3899 15.
三、解答题:本大题共6小题,共75分.
16.(本小题满分12分)
解:(1)


 ……3分
……3分 ……4分
……4分
令

 的单调区间
的单调区间 ,k∈Z ......6分
,k∈Z ......6分
(2)由 得
得 
 .....7分
.....7分
又 为
为 的内角
的内角

 ......9分
......9分


 ...11分
...11分

 ....12分
....12分
17. (本小题满分12分)
解:(1)记“甲击中目标的次数减去乙击中目标的次数为2”为事件A,则
 ,解得
,解得 .....4分
.....4分
(2) 的所有可能取值为0,1,2.记“在第一次射击中甲击中目标”为事件
的所有可能取值为0,1,2.记“在第一次射击中甲击中目标”为事件 ;记“在第一次射击中乙击中目标”为事件
;记“在第一次射击中乙击中目标”为事件 .
.
则 ,
,

 ,.....10分
,.....10分
所以 的分布列为
的分布列为

0
1
2
P



∴ =
= .....12分
.....12分
18. (本小题满分12分)
解:(1)当 为
为 中点时,有
中点时,有 平面
平面
证明:连结 交
交 于
于 ,连结
,连结
∵四边形 是矩形 ∴
是矩形 ∴ 为
为 中点
中点
又 为
为 中点,从而
中点,从而
∵ 平面
平面 ,
, 平面
平面
∴ 平面
平面 .....4分
.....4分
(2)建立空间直角坐标系 如图所示,
如图所示,
则 ,
, ,
, ,
, ,
,
.....6分
所以 ,
, .
.
设 为平面
为平面 的法向量,则有
的法向量,则有 ,即
,即
令 ,可得平面
,可得平面 的一个法向量为
的一个法向量为 ,.....9分
,.....9分
而平面 的一个法向量为
的一个法向量为 .....10分
.....10分
所以
所以二面角 的余弦值为
的余弦值为 .....12分
.....12分
(用其它方法解题酌情给分)
19.(本小题满分13分)
解:(1)由题意知

因此数列 是一个首项
是一个首项 .公比为3的等比数列,所以
.公比为3的等比数列,所以 ......2分
......2分
 又
又
 =100―(1+3+9)
=100―(1+3+9)
所以 =87,解得
=87,解得
因此数列 是一个首项
是一个首项 ,公差为―5的等差数列,
,公差为―5的等差数列,
所以  .....4分
.....4分
(2) 求视力不小于5.0的学生人数为 .....7分
.....7分
(3) 由 ①
①
可知,当 时,
时, ②
②
①-②得,当 时,
时, ,
,
 , .....11分
, .....11分
又
因此数列 是一个从第2项开始的公比为3的等比数列,
是一个从第2项开始的公比为3的等比数列,
数列 的通项公式为
的通项公式为 .....13分
.....13分
20.(本小题满分13分)
解:(1)由于 ,
,
∴ ,解得
,解得 ,
,
∴椭圆的方程是 .....3分
.....3分
(2)∵ ,∴
,∴ 三点共线,
三点共线,
而 ,设直线的方程为
,设直线的方程为 ,
,
由 消去
消去 得:
得: 
由 ,解得
,解得 .....6分
.....6分
设 ,由韦达定理得
,由韦达定理得 ①,
①,
又由 得:
得: ,∴
,∴ ②.
②.
将②式代入①式得: ,
,
消去 得:
得: .....10分
.....10分
设 ,当
,当 时,
时,  是减函数,
是减函数,
∴ , ∴
, ∴ ,
,
解得 ,又由
,又由 得
得 ,
,
∴直线AB的斜率的取值范围是 .....13分
.....13分
21. (本小题满分13分)
(1)解:
①若
∵ ,则
,则 ,∴
,∴ ,即
,即 .
.
∴ 在区间
在区间 是增函数,故
是增函数,故 在区间
在区间 的最小值是
的最小值是
.....2分
②若
令 ,得
,得 .
.
又当 时,
时, ;当
;当 时,
时, ,
,
∴ 在区间
在区间 的最小值是
的最小值是 .....4分
.....4分
(2)证明:当 时,
时, ,则
,则 ,
,
∴ ,
,
当 时,有
时,有 ,∴
,∴ 在
在 内是增函数,
内是增函数,
∴ ,
,
∴ 在
在 内是增函数,
内是增函数,
∴对于任意的 ,
, 恒成立.....7分
恒成立.....7分
(3)证明:
 ,
,
令
则当 时,
时, ≥
≥
 ,.....10分
,.....10分
令 ,则
,则 ,
,
当 时,
时,  ;当
;当 时,
时, ;当
;当 时,
时, ,
,
则 在
在 是减函数,在
是减函数,在 是增函数,
是增函数,
∴ ,
,
∴ ,
,
∴ ,即不等式
,即不等式 ≥
≥ 对于任意的
对于任意的 恒成立.....13分
恒成立.....13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com