9、欢欢到商店买一块手帕（四边形），为了检验这块手帕是否是方的（正方形），她的做法如下：第①步：分别以对角线为折叠线进行折叠，结果另两个顶点都能互相重合；第②步：以一组对边的中点所在的直线为折叠线进行折叠，四个顶点两两重合．结果欢欢认定这块手帕是方的．其中步骤①验证了手帕是（填“平行四边形”、“矩形”或“菱形”）．

操作与探究：
在八年级探究“直角三角形斜边上的中线等于斜边的一半”这个结论时，我们是将一块直角三角形纸片按照图①方法折叠（点A与点C重合，DE为折痕）．再将图①中的△CBE沿对称轴EF折叠（如图②），通过折叠，可以发现CE=AE=BE=

1

2

AB．
（1）在上述的折叠过程中，我们还可以发现原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（2）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足什么条件时，一定能折成组合矩形？
满足的条件是．

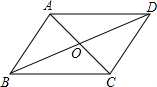如图，长度不等的两根牙签AC、BD的中点O重合，问顺次连接各端点A、B、C、D所得四边形是什么特殊四边形？为什么？请补充完成下面的解答过程．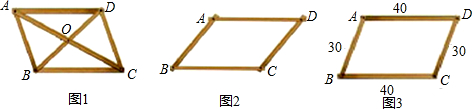
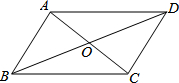解：所得四边形ABCD为
理由如下：因为O为AC、BD的中点
所以OA=，OB=
所以四边形ABCD为
根据是．

（1）小明的爸爸在钉制平行四边形框架时，采用了下面的两种方法．
方法一：如图1，将两根木条AC、BD中点重叠，并用钉子固定，则四边形ABCD就是平行四边形．这样做的依据是：．
方法二：如图2，将两根同样长的木条AB、CD平行放置，再木条AD、BC加固，则四边形ABCD就是平行四边形．
这样做的依据是：．
方法三：如图3，用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边，并把相等的木条作为相对的边用钉子固定，则四边形ABCD就是平行四边形．这样做的依据是：．

（2）2002年世界数学家大会（ICM-2002）在北京召开，这节大会的会标的中央图案是经过艺术处理的“弦图”，它既标志着中国古代的数学成就，又像一只转动的风车，欢迎来自世界各地的数学家们!在这个“弦图”中，隐含着我们学过的一个重要的数学定理，这个定理可以用含a、b、c的等式来表示，它是：．

如图，我们使长度不等的两根牙签AC、BD的中点O重合，那么顺次连接各端A、B、C、D所得四边形是什么特殊四边形？你如何判断的？（请补充完成下面的解答过程）
解：所得四边形ABCD为
用文字表达依据是
用数学符号表示理由如下：