⑴　在同一平面内，__的两条直线叫做平行线．若直线__ 与直线 __平行，则记作_．
⑵　在同一平面内，两条直线的位置关系只有_____、_____．
⑶　平行公理是：____________________________________________．
⑷　平行公理的推论是如果两条直线都与______，那么这两条直线也______．即三条直线a,b,c，若a∥b,b∥c，则______．
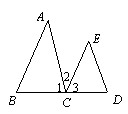
⑸　已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．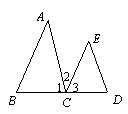

⑴∵ ∠B=∠3(已知)，∴______∥______.(______，______)
⑵∵∠1=∠D (已知)，∴______∥______.(______，______)
⑶∵∠2=∠A (已知)，∴______∥______.(______，______)
⑷∵∠B+∠BCE=180° (已知)，∴______∥______.(______，______)

（本小题满分8分）
　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；
（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

（本小题满分8分）

　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；

（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．