
题目列表(包括答案和解析)
 -6b2+3被墨水弄脏了,请问横线上的一项是( )
-6b2+3被墨水弄脏了,请问横线上的一项是( ) ﹣6b2+3被墨水弄脏了,请问横线上的一项是
﹣6b2+3被墨水弄脏了,请问横线上的一项是 -6b2+3被墨水弄脏了,请问横线上的一项是
-6b2+3被墨水弄脏了,请问横线上的一项是解方程组 的最好方法是(
)
的最好方法是(
)
A.由①得 ,代入② B.由②得
,代入② B.由②得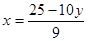 ,代入①
,代入①
C.由①得 ,代入② D.由②得
,代入② D.由②得 ,代入①
,代入①
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com