练习册

  • 练习册
  • 试题
    本节课安排了三个例题.例1是教材P118中的例1．它是等腰梯形性质的直接运用．题目比较简单.在教学中.最好让学生分析.讲解.解答．同时也要注意引导学生.在证明△EAD是等腰三角形时.要用到梯形的定义“上下底互相平行 这一点． 例2与例3都是补充的题目.例2是一道计算题.例3是一道证明题.其用意一是为了巩固其概念.二是辅助线添加方法的练习.这两个题目的辅助线均是“平移一腰 .老师们在教学或练习中也可以再补充一些其它辅助线添加方法的题目.让学生多了解多见识．(但由于本教材在梯形这一部分知识中.并没有添加辅助线的要求.因此所选的题目不要太难．)通过题目的练习与讲解应让学生知道:解决梯形问题的基本思想和方法就是通过添加适当的辅助线.把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．在教学时应让学生注意它们的作用.掌握这些辅助线的使用对于学好梯形内容很有帮助． 【查看更多】

     

    题目列表(包括答案和解析)

    下列命题中，真命题是（　　）
    A、如果三角形三个角的度数比是3：4：5，那么这个三角形是直角三角形；
    B、如果直角三角形两直角边的长分别为a和b，那么斜边的长为a2+b2；
    C、若三角形三边长的比为1：2：3，则这个三角形是直角三角形；
    D、如果直角三角形两直角边分别为a和b，斜边为c，那么斜边上的高h的长为
    ab
    c

    查看答案和解析>>

    下列命题中，真命题是（　　）
    A．如果三角形三个角的度数比是3：4：5，那么这个三角形是直角三角形；
    B．如果直角三角形两直角边的长分别为a和b，那么斜边的长为a2+b2；
    C．若三角形三边长的比为1：2：3，则这个三角形是直角三角形；
    D．如果直角三角形两直角边分别为a和b，斜边为c，那么斜边上的高h的长为
    ab
    c

    查看答案和解析>>

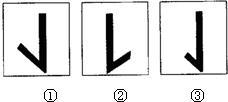    某天，小刚选择了三个不同的时间，在木杆南面的相同位置给木杆照了三张照片，如图所示，那么三张照片照的先后顺序正确的是（　　）

    查看答案和解析>>

    小明根据下表，作了三个推测：
    x 1 10 100 1000 10000 …
    6+
    1
    x
    		 7 6.1 6.01 6.001 6.0001 ••
    ①6+
    1
    x
    （x＞0）的值随着x的增大越来越小；
    ②6+
    1
    x
    （x＞0）的值有可能等于6；
    ③6+
    1
    x
    （x＞0）的值随着x的增大越来越接近于6．其中，推测正确的有（　　）
    A、3个B、2个C、1个D、0个

    查看答案和解析>>

    晓晓根据下表，作了三个推测：
    x   1 10  100  1000   10000 …
     3-
    x-1
    x
    		 3   2.1  2.01  2.001  2.0001 …
    ①3-
    x-1
    x
    （x＞0）的值随着x的增大越来越小；
    ②3-
    x-1
    x
    （x＞0）的值有可能等于2；
    ③3-
    x-1
    x
    （x＞0）的值随着x的增大越来越接近于2．
    则推测正确的有（　　）
    A、0个B、1个C、2个D、3个

    查看答案和解析>>


    同步练习册答案