
题目列表(包括答案和解析)
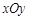 中,抛物线
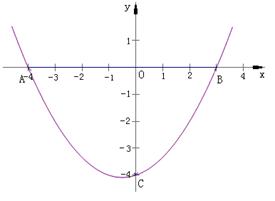
中,抛物线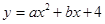 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
在平面直角坐标系 中,抛物线
中,抛物线 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
【小题1】求该抛物线的解析式;
【小题2】若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
【小题3】该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
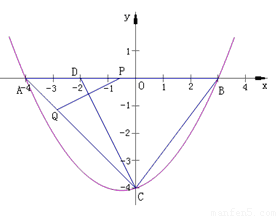
如图,抛物线经过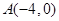 ,
, ,
,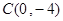 三点.
三点.
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上存在一点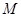 ,使
,使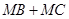 的值最小,求点
的值最小,求点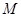 的坐标以
的坐标以
及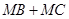 的最小值;
的最小值;
(3)在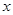 轴上取一点
轴上取一点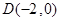 ,连接
,连接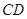 .现有一动点
.现有一动点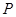 以每秒
以每秒 个单位长度的速度从点
个单位长度的速度从点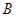 出发,沿线段
出发,沿线段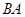 向点
向点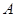 运动,运动时间为
运动,运动时间为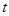 秒,另有一动点
秒,另有一动点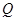 以某一速度同时从点
以某一速度同时从点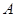 出发,沿线段
出发,沿线段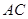 向点
向点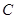 运动,当点
运动,当点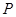 、点
、点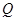 两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个
两点中有一点到达终点时,另一点则停止运动(如右图所示).在运动的过程中是否存在一个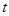 值,使线段
值,使线段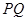 恰好被
恰好被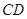 垂直平分.如果存在,请求出
垂直平分.如果存在,请求出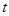 的值和点
的值和点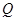 的速度,如果不存在,请说明理由.
的速度,如果不存在,请说明理由.
【解析】此题主要考查了用待定系数法求二次函数解析式,以及利用函数图象和图象上点的性质判断符合某一条件的点是否存在,是一道开放性题目,有利于培养同学们的发散思维能力
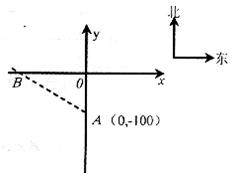
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即![]() /s).交通管理部门在离该公路100m处设置了一速度监测点A,在如图的坐标系中,点A位于y轴上,测速路段BC在
/s).交通管理部门在离该公路100m处设置了一速度监测点A,在如图的坐标系中,点A位于y轴上,测速路段BC在![]() 轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)请在图中画出表示北偏东45°方向的射线AC,并标出点C的位置;
(2)点B的坐标为________________,点C的坐标为_______________________;
(3)一辆汽车从点B行驶到点C所用的时间为15s,请通过计算,判断该汽车在限速公路上是否超速行驶?(本小题![]() 取1.7)
取1.7)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com