
题目列表(包括答案和解析)
 31、阅读下面的题目及分析过程,并按要求进行证明.
31、阅读下面的题目及分析过程,并按要求进行证明.

 21、如图,△ABC中,①AB=AC,②∠BAD=∠CAD,③BD=CD,④AD⊥BC.请你选择其中的两个作为条件,另两个作为结论,证明等腰三角形的“三线和一”性质定理.
21、如图,△ABC中,①AB=AC,②∠BAD=∠CAD,③BD=CD,④AD⊥BC.请你选择其中的两个作为条件,另两个作为结论,证明等腰三角形的“三线和一”性质定理.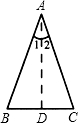 “等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.
“等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合”的定理是将“等腰三角形”作为一个不变的已知条件参与组合得到的三个真命题,在学习了等腰三角形的判定后,可将该定理作如下的引伸.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com