
题目列表(包括答案和解析)
 如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:
如图,AD为⊙O的直径,作⊙O的内接等边三角形ABC.黄皓、李明两位同学的作法分别是:

如图,已知线段AB。

(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
某校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12. 请你回答:
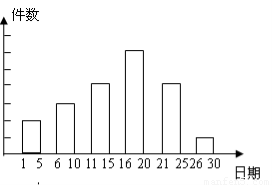
(1)本次活动共有__________件作品参赛;各组作品件数的中位数是_________件.
(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?
(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com