练习册

  • 练习册
  • 试题
    3．合作探究 (1)整体感知 请同学们先将这个命题画出图形.写出已知.求证． (2)四边互动 互动1 师:这又是证明线段相等的命题.回忆上节课证明角平分线性质定理的方法.会得到什么启发? 生:可以利用S．A．S．定理证明△PAC≌△PBC.从而得到PA=PB． 师:很好．这样就得到了线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端点距离相等． 今后我们可以直接利用这个定理直接得到有关线段相等.同时这也可当作等腰三角形的一种判定方法． 明确 巩固利用三角形全等来证明线段相等的方法． 互动2 师:反过来.到一条线段的两个端点的距离相等的点是否一定在这条线段的垂直平分线上呢?我们也可以通过“证明 来解决这个问题． 生:画出图形.写出已知.求证． 师:为了证明Q点在AB的垂直平分线上.可以过Q作辅助线.先构造“垂直或平分 中的一个关系.去证明另一个．特别要注意防止“过Q作线段AB的垂直平分线 这种错误．你能根据提示.说出证明过程吗? 生:(略) 师:在证明过程中.很巧妙地利用了前面学习过的等腰三角形“三线合一 的性质.看来同学们能够学以致用.这一点很好．这样我们又得到了线段垂直平分线的判定定理:到一条线段两端点距离相等的点.在这条线段的垂直平分线上． 生:判定定理只能判断点在线段垂直平分线上.那怎么才能判断这条直线就是线段的垂直平分线呢? 师:这个问题提得很好．大家想一想.几点确定一条直线? 生:两点． 师:所以.只要我们能证明一条直线上有两点满足判定定理的条件.那么这条直线就一定是线段的垂直平分线． 明确 利用等腰三角形“三线合一 证明的方法值得重视． 例:已知:如图所示.△ABC中.m.n.L分别是BC.AC.AB边上的垂直平分线.求证:m.n.L必交于一点． 证明:设m.n交于一点O.连接OA.OB.OC． 则有OA=OB=OC(线段垂直平分线上的点到线段两端的距离相等) 因为OA=OB 所以O在L上(到线段两端距离相等的点在线段的垂直平分线上) 即m.n.L交于一点 明确 巩固证明“三线共点 的方法． 师:这道例题的结论又告诉我们.三角形的三条边的垂直平分线也交于一点.这一点称为三角形的外心.外心的性质是到三角形的三个顶点的距离相等． 【查看更多】

     

    题目列表(包括答案和解析)

    求一个正数的算术平方根，有些数可以直接求得，如
    		4
    ，有些数则不能直接求得，如
    		7
    ．但可以利用计算器求得，还可以通过一组数的内在联系，运用规律求得．
    请同学们观察下表：
    n 0.09 9 900 90000 …
    		n
    		 0.3 3 30 300 …
    运用你发现的规律解决问题，已知
    		2.06
    ≈1.435，则
    		206
    ≈    （　　）

    查看答案和解析>>

    某年中考，所用准考证号共有7位，设定末尾用1表示男生，用2表示女生．比如，0113141表示“2001年参加考试，考场为第13考场，座位号为14号，男生．”那么，请同学们想一想：“0202022”表示的含义是（　　）

    查看答案和解析>>

    9、小芳步行上学，最初以某一速度匀速前进，中途遇红灯，稍作停留后加快速度跑步去上学，到校后，她请同学们画出她行进路程s（米）与行进时间t（分钟）的函数图象的示意图．你认为正确的是（　　）

    查看答案和解析>>

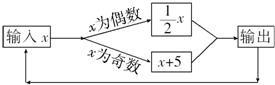    精英家教网2008年8月8日晚上8时，第29届奥运会开幕式在北京“鸟巢”举行，开幕式宏伟壮观，大气磅礴，给世人留下了深刻的印象，据悉，这部盛典的幕后工作者是中国航天人，他们使用了大量载人航天技术和火箭技术，给奥运场馆装上了“大脑”，实现“不同地域、不同场馆”的信息集成，以保证零失误，可想而知，其中的程序设计多么复杂．现在请同学们体会一个小小的程序设计．如图，若开始输入的x值为96，我们发现得到的结果为48，第2次得到的结果为24…，通过探索可知，第2009次得到的结果为（　　）
    A、3B、6C、8D、1

    查看答案和解析>>

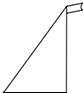    数学实践探究课中，老师布置同学们测量学校旗杆的高度．如图所示，小明所在的学习小组在距离旗杆底部10米的地方，用测角仪测得旗杆顶端的仰角为60°，则旗杆的高度是（　　）米．

    查看答案和解析>>


    同步练习册答案