
题目列表(包括答案和解析)
 同学们,第二章我们学习了两类特殊三角形:直角三角形和等腰三角形.其实这两类三角形是可以互相转化的,任意一个等腰三角形可以分割成两个全等的直角三角形,而任意一个直角三角形也可以分割成两个等腰三角形,现在请用直尺和圆规找到一条直线,把Rt△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹).
同学们,第二章我们学习了两类特殊三角形:直角三角形和等腰三角形.其实这两类三角形是可以互相转化的,任意一个等腰三角形可以分割成两个全等的直角三角形,而任意一个直角三角形也可以分割成两个等腰三角形,现在请用直尺和圆规找到一条直线,把Rt△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹).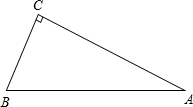 同学们,第二章我们学习了两类特殊三角形:直角三角形和等腰三角形.其实这两类三角形是可以互相转化的,任意一个等腰三角形可以分割成两个全等的直角三角形,而任意一个直角三角形也可以分割成两个等腰三角形,现在请用直尺和圆规找到一条直线,把Rt△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹).
同学们,第二章我们学习了两类特殊三角形:直角三角形和等腰三角形.其实这两类三角形是可以互相转化的,任意一个等腰三角形可以分割成两个全等的直角三角形,而任意一个直角三角形也可以分割成两个等腰三角形,现在请用直尺和圆规找到一条直线,把Rt△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com