
题目列表(包括答案和解析)

. |
| abc |
. |
| abc |
. |
| ab |
. |
| abcd |
. |
| abcd |
. |
| abc |
. |
| ab |
我们知道,平方差公式是: (a+b)(a-b) = a2 - b2,反过来得到:a2 - b2=(a+b)(a-b)也成立,在解决某些问题时逆用平方差公式会起到很好的效果,如:计算:
根据平方差逆用方法,请计算下列各题:
(1) 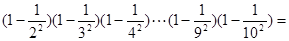 ;(2分)
;(2分)
(2) 正整数m、n满足m2- n2=7,求m、n的值.(3分)
我们知道,平方差公式是: (a+b)(a-b) = a2 - b2,反过来得到:a2 - b2=(a+b)(a-b)也成立,在解决某些问题时逆用平方差公式会起到很好的效果,如:计算:
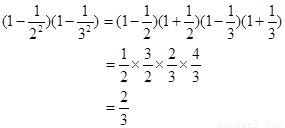
根据平方差逆用方法,请计算下列各题:
(1) 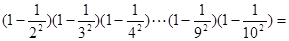 ;(2分)
;(2分)
(2) 正整数m、n满足m2 - n2 =7,求m、n的值.(3分)
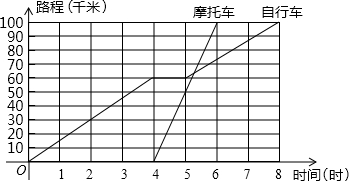
 是一个三位的自然数,已知
是一个三位的自然数,已知 ,这个三位数是218;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果
,这个三位数是218;聪明的小亮在解决这种问题时,采取列成连减竖式的方法(见右图)确定要求的自然数,请你仿照小亮的作法,解决这种问题.如果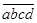 是一个四位的自然数,且
是一个四位的自然数,且  ,那么,这个四位数是_____________.
,那么,这个四位数是_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com